Trong bài trước, chúng ta đã tìm hiểu về Gradient Descent – một phương pháp tối ưu hóa phổ biến trong Machine Learning. Tiếp tục chuỗi bài học, bài này chúng ta sẽ tìm hiểu về mô hình Hồi quy Logistic (Logistic Regression), một thuật toán phổ biến dùng cho bài toán phân loại nhị phân.
Logistic Regression là gì?
Hồi quy Logistic là một mô hình thống kê được sử dụng để phân loại nhị phân, tức dự đoán một đối tượng thuộc vào một trong hai nhóm. Hồi quy Logistic làm việc dựa trên nguyên tắc của hàm sigmoid – một hàm phi tuyến tự chuyển đầu vào của nó thành xác suất thuộc về một trong hai lớp nhị phân.
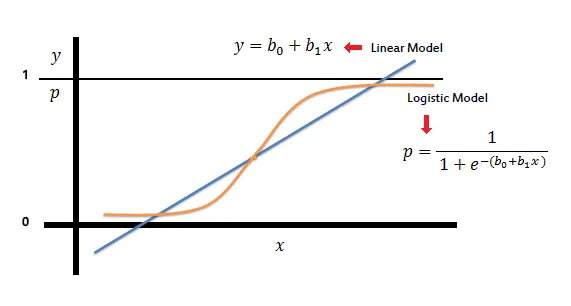
Hồi quy Logistic hoạt động dựa trên hàm Sigmoid, được biểu diễn như sau:
Hàm Sigmoid nhận đầu vào là một giá trị z bất kỳ, và trả về đầu ra là một giá trị xác suất nằm trong khoảng [0, 1]. Khi áp dụng vào mô hình Hồi quy Logistic với đầu vào là ma trận dữ liệu X và trọng số w, ta có z = Xw.
Việc huấn luyện của mô hình là tìm ra bộ trọng số w sao cho đầu ra dự đoán của hàm Sigmoid gần với kết quả thực tế nhất. Để làm được điều này, ta sử dụng hàm mất mát (Loss Function) để đánh giá hiệu năng của mô hình. Mô hình càng tốt khi hàm mất mát càng nhỏ.
Hàm mất mát (Loss Function) là một hàm số được sử dụng để đo lường mức độ lỗi mà mô hình của chúng ta tạo ra khi dự đoán các kết quả từ dữ liệu đầu vào. Trong bài toán Hồi quy Logistic, chúng ta sử dụng hàm mất mát Cross-Entropy (còn gọi là Log Loss) để đánh giá hiệu năng của mô hình.
Hàm mất mát Cross-Entropy được định nghĩa như sau:
L(w) = -\frac{1}{n} \sum_{i=1}^{n} [y_i \log p_i + (1 - y_i) \log (1 - p_i)],
Trong đó:
- n: số lượng mẫu dữ liệu trong tập huấn luyện.
- y_i: giá trị thực tế của đầu ra thứ i.
- p_i: xác suất dự đoán thuộc lớp 1 của mô hình cho đầu vào thứ i.
Hàm Cross-Entropy đo lường khoảng cách giữa hai phân phối xác suất y_i và p_i. Khi mô hình dự đoán chính xác, tức là nếu y_i = 1 thì p_i càng gần 1, và nếu y_i = 0 thì p_i càng gần 0, sau đó hàm mất mát sẽ tiến gần về 0.
Trong quá trình huấn luyện, chúng ta tìm cách cập nhật bộ trọng số w sao cho giá trị hàm mất mát Cross-Entropy đạt giá trị nhỏ nhất, dẫn đến một mô hình dự đoán tốt nhất.
Để tìm giá trị tối ưu cho bộ trọng số w, chúng ta có thể sử dụng kỹ thuật Gradient Descent. Tại mỗi bước lặp, chúng ta cập nhật w theo phương từm ứng với đạo hàm của hàm mất mát L(w) theo w.
Ví dụ ứng dụng Logistic Regression
Hãy cùng xem xét một ví dụ kinh điển trong Machine Learning, đó là việc dự đoán rủi ro mắc bệnh tiểu đường của bệnh nhân dựa trên dữ liệu về sức khỏe của họ.
Dữ liệu bao gồm các thông tin như: tuổi, giới tính, chỉ số khối cơ thể, huyết áp, mức đường huyết, và biến mục tiêu là việc bệnh nhân có mắc bệnh tiểu đường hay không (1 là có, 0 là không).
Chúng ta sẽ chia dữ liệu thành hai tập: tập huấn luyện (80% dữ liệu) và tập kiểm tra (20% dữ liệu). Tiếp đó, sử dụng Logistic Regression để xây dựng mô hình dự đoán rủi ro mắc bệnh tiểu đường dựa trên số liệu từ tập huấn luyện.
Sau khi đã tìm ra bộ trọng số w tối ưu bằng cách tối ưu hóa hàm mất mát của mô hình, chúng ta sẽ sử dụng mô hình này để dự đoán các trường hợp mới trong tập kiểm tra. Đánh giá hiệu năng của mô hình bằng cách tính tỉ lệ các dự đoán chính xác của mô hình so với kết quả thực tế.
Công thức toán
Trong quá trình học và làm việc với Hồi quy Logistic, chúng ta cần nắm vững một số công thức toán quan trọng như sau:
Hàm sigmoid:
S(z) = 1 / (1 + e^{-z})Xác suất thuộc lớp 1 cho mỗi ví dụ:
P(y=1|X)=S(Xw)Hàm mất mát cross-entropy (sử dụng cho Logistic Regression):
L(w) = -\frac{1}{n} \sum_{i=1}^{n} [y_i \log p_i + (1 - y_i) \log (1 - p_i)]Gradient của hàm mất mát (đạo hàm theo w của hàm mất mát):
\nabla L(w) = \frac{1}{n} X^T (S(Xw) - Y)Sử dụng các công thức trên, chúng ta có thể huấn luyện mô hình Hồi quy Logistic và dự đoán kết quả cho dữ liệu mới.
Ví dụ code Python
Để minh họa cách xây dựng mô hình Hồi quy Logistic trong Python, chúng ta sẽ sử dụng thư viện numpy để tính toán và sklearn để chia dữ liệu và đánh giá mô hình:
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
# Hàm sigmoid
def sigmoid(z):
return 1 / (1 + np.exp(-z))
# Hàm mất mát (Loss Function)
def loss_function(y, p):
return -np.mean(y * np.log(p) + (1 - y) * np.log(1 - p))
# Gradient Descent
def gradient_descent(X, y, learning_rate, n_iterations):
n_samples, n_features = X.shape
w = np.zeros((n_features, 1))
y = y.reshape((-1, 1))
for _ in range(n_iterations):
z = np.dot(X, w)
p = sigmoid(z)
gradient = np.dot(X.T, (p - y)) / n_samples
w -= learning_rate * gradient
return w
# Hàm dự đoán
def predict(X, w):
p = sigmoid(np.dot(X, w))
return (p > 0.5).astype(int)
# Load dữ liệu và tiền xử lý
X, y = load_your_data()
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# Huấn luyện mô hình
w = gradient_descent(X_train, y_train, learning_rate=0.01, n_iterations=1000)
# Dự đoán và đánh giá mô hình
y_pred = predict(X_test, w)
print("Accuracy score:", accuracy_score(y_test, y_pred))
Như vậy, chúng ta đã xây dựng thành công mô hình Hồi quy Logistic sử dụng Gradient Descent để huấn luyện và dự đoán kết quả cho bài toán phân loại nhị phân.
Lưu ý: Trong thư viện scikit-learn, đã có sẵn lớp LogisticRegression để giúp chúng ta giải quyết các bài toán tương tự một cách nhanh chóng và hiệu quả hơn.
Hi vọng thông qua bài viết các bạn đã hiểu thêm về Logistic Regression, một trong những kỹ thuật cơ bản của Machine Learning. Hẹn gặp lại các bạn trong các bài tiếp theo của chuối bài học Machine Learning Cơ bản.
