Bài 5: Gradient Descent

trituenhantao.io

7 tháng trước

Trong bài trước, chúng ta đã tìm hiểu về K-means Clustering, một thuật toán học máy không giám sát. Trong bài này, chúng ta sẽ tìm hiểu về Gradient Descent – một thuật toán tối ưu hóa được sử dụng trong phổ biến lĩnh vực của Machine Learning .

1. Giới thiệu về Gradient Descent

Gradient Descent là một trong các thuật toán tối ưu hóa phổ biến nhất, đặc biệt là trong lĩnh vực Machine Learning . Thuật toán này dựa trên việc tìm kiếm cực trị (cực đại hoặc cực tiểu) của một hàm số bằng cách tính đạo hàm và di chuyển theo hướng giảm dần của gradient .

Ý tưởng của gradient descent là tính đạo hàm và di chuyển theo hướng giảm dần của gradient .

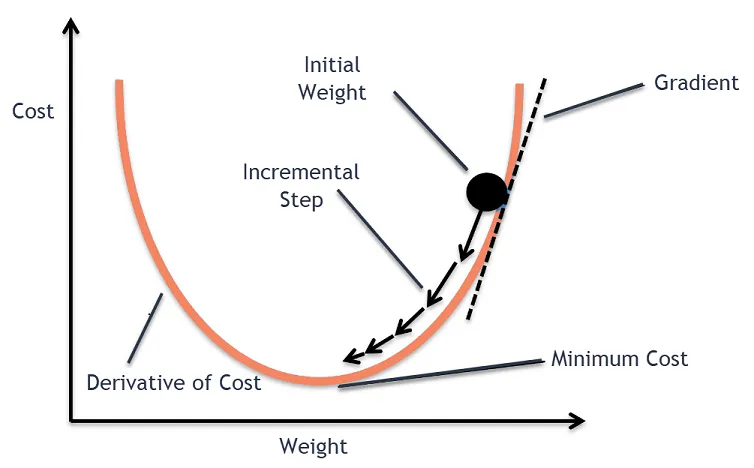
2. Hàm một biến

Xét hàm một biến $f(x)$ . Thuật toán Gradient Descent tìm cực tiểu của hàm số bằng cách khởi tạo giá trị $x$ tại một vị trí ngẫu nhiên, sau đó di chuyển $x$ ngược hướng với đạo hàm của $f(x)$ . Thao tác này sẽ được lặp lại cho đến khi đạt đến một ngưỡng nào đó.

Công thức cập nhật $x$ trong Gradient Descent:

x _{t+1} = x_t - \alpha * f'(x_t)

Trong đó:

$x_{t}$ là giá trị $x$ tại bước thứ $t$ ,
$\alpha$ là learning rate (tốc độ học),
$f'(x_t)$ là đạo hàm của hàm $f$ tại $x_t$ .

3. Hàm nhiều biến

Đối với một hàm nhiều biến $f(\vec{x})$ , thuật toán này sẽ tính Gradient (vector đạo hàm) của hàm $f$ tại một điểm ngẫu nhiên $\vec{x}$ , sau đó di chuyển $\vec{x}$ ngược hướng với Gradient này.

Công thức cập nhật $\vec{x}$ :

\vec{x}_{t+1} = \vec{x_t} - \alpha * \nabla{f(\vec{x}_t)}

Trong đó:

$\vec{x}_{t}$ là giá trị $\vec{x}$ tại bước thứ $t$ ,
$\alpha$ là learning rate (tốc độ học),
$\nabla{f(\vec{x}_t)}$ là Gradient của hàm $f$ tại $\vec{x}_t$ .

4. Các thuật toán Gradient Descent

Có nhiều biến thể của thuật toán này tuỳ thuộc vào việc lựa chọn dữ liệu huấn luyện và thứ tự cập nhật:

Batch Gradient Descent: Sử dụng toàn bộ dữ liệu huấn luyện để cập nhật $\vec{x}$ trong mỗi bước lặp. Thuật toán này có độ chính xác cao nhưng mất nhiều thời gian do tính toán trên toàn bộ dữ liệu.
Stochastic Gradient Descent (SGD): Sử dụng chỉ một điểm dữ liệu huấn luyện ngẫu nhiên để cập nhật $\vec{x}$ . Tốc độ hội tụ nhanh hơn, nhưng độ chính xác thấp hơn so với Batch Gradient Descent.
Mini-batch Gradient Descent: Sử dụng một số lượng nhỏ điểm dữ liệu huấn luyện (mini-batch ) để cập nhật $\vec{x}$ . Kết hợp ưu điểm của cả Batch Gradient Descent và SGD.

5. Biến thể

Một số cải tiến của Gradient Descent để tăng tốc độ hội tụ và giảm thiểu dao động trong quá trình hội tụ:

Momentum: Giảm dao động qua lại của gradient và đi nhanh hơn dọc theo hướng tiến.
Nesterov Accelerated Gradient (NAG): Sử dụng momentum bằng cách tính gradient trước khi cập nhật vị trí của $\vec{x}$ .
Adaptive Gradient (Adagrad): Đưa vào learning rate riêng cho mỗi parameter.
Adaptive Moment Estimation (Adam): Kết hợp momentum và adaptive learning rate .

6. Điều kiện dừng của Gradient Descent

Một số điều kiện dừng thường được cài đặt:

Số lượng vòng lặp cố định: Dừng sau một số lượng lần cập nhật $\vec{x}$ cố định.
Đạo hàm tiệm cận 0: Dừng khi đạo hàm của hàm $f$ tiệm cận 0 ở mỗi biến.
Thay đổi của hàm tiệm cận 0: Dừng khi thay đổi của hàm $f$ qua mỗi bước lặp tiệm cận 0.

7. Newton Method

Một phương pháp tối ưu hóa khác là Newton Method, sử dụng đạo hàm cấp 2 (Hessian matrix) của hàm $f$ . Thuật toán này tìm ra vị trí cực tiểu của hàm $f$ nhanh hơn so với Gradient Descent, nhưng cần phải tính Hessian matrix, có độ phức tạp tính toán cao hơn.

Công thức cập nhật $\vec{x}$ trong Newton Method:

\vec{x}_{t+1} = \vec{x}_t - \left[ \nabla^2f(\vec{x}_t) \right]^{-1} \nabla{f(\vec{x}_t)}

Trong đó:

\vec{x}<em>{t+1}

và

\vec{x}</em>{t}

là giá trị $\vec{x}$ tại bước thứ ${t+1, t}$ , $\nabla^2f(\vec{x}_t)$ là Hessian matrix của hàm $f$ tại $\vec{x}_t$ , $\nabla{f(\vec{x}_t)}$ là Gradient của hàm $f$ tại $\vec{x}_t$ .

8. Ví dụ minh họa với Python

Dưới đây là một ví dụ minh họa sử dụng Gradient Descent để tìm cực tiểu của hàm số:

f(x) = (x-4)^2 + 6

Đạo hàm của hàm số:

f'(x) = 2(x-4)

Ta có thể sử dụng Gradient Descent để tìm cực tiểu của hàm này như sau:

import numpy as np

# Định nghĩa hàm f(x) và đạo hàm f'(x)
def f(x):
    return (x - 4) ** 2 + 6

def df(x):
    return 2 * (x - 4)

# Khởi tạo giá trị x ban đầu
x_t = np.random.randn()
print("Giá trị x ban đầu: ", x_t)

# Thiết lập tốc độ học alpha và số bước lặp
alpha = 0.1
max_iterations = 100

# Gradient Descent
for t in range(max_iterations):
    x_t1 = x_t - alpha * df(x_t) # Cập nhật giá trị x

    # Kiểm tra đạo hàm tiệm cận 0 (Tức điểm cực tiểu)
    if np.abs(df(x_t1)) < 1e-6:
        break

    x_t = x_t1

print("Giá trị x tối ưu: ", x_t)
print("Giá trị cực tiểu của hàm f(x): ", f(x_t))

Kết quả sẽ cho thấy giá trị $x$ tối ưu và giá trị cực tiểu của hàm số sau khi áp dụng Gradient Descent.

Qua ví dụ trên, chúng ta đã thấy cách áp dụng Thuật toán Gradient Descent để tìm cực tiểu của một hàm số đơn giản. Tương tự, chúng ta có thể áp dụng nó trong các bài toán Machine Learning phức tạp hơn như Linear Regression, Logistic Regression và Neural Networks.

Sau khi nắm vững kiến thức về các thuật toán tối ưu hóa như Gradient Descent và Newton Method, chúng ta có thể áp dụng chúng vào các bài toán thực tế trong Machine Learning để giải quyết các vấn đề phức tạp với hiệu suất cao. Điều này sẽ giúp chúng ta tiến gần hơn đến việc giái quyết các bài toán phức tạp của thế giới thực và đưa ra các dự đoán chính xác dựa trên dữ liệu thật. Hãy tiếp tục theo dõi chuỗi bài học Machine learning Cơ bản của trituenhantao.io để cập nhật thêm các kiến thức cơ bản về lĩnh vực.