Bài 3: Linear Regression (Hồi quy tuyến tính)

🔊 Nghe bài viết

Giới thiệu

Trong bài trước, chúng ta đã tìm hiểu về các thuật toán Machine Learning cơ bản. Bài này chúng ta sẽ tìm hiểu về một trong những thuật toán phổ biến nhất trong Machine Learning – Linear Regression (Hồi quy tuyến tính). Linear Regression được ứng dụng rộng rãi trong nhiều lĩnh vực, từ dự báo giá cả, điểm số, đầu ra sản xuất đến dữ liệu chuỗi thời gian (time series), và nhiều lĩnh vực khác.

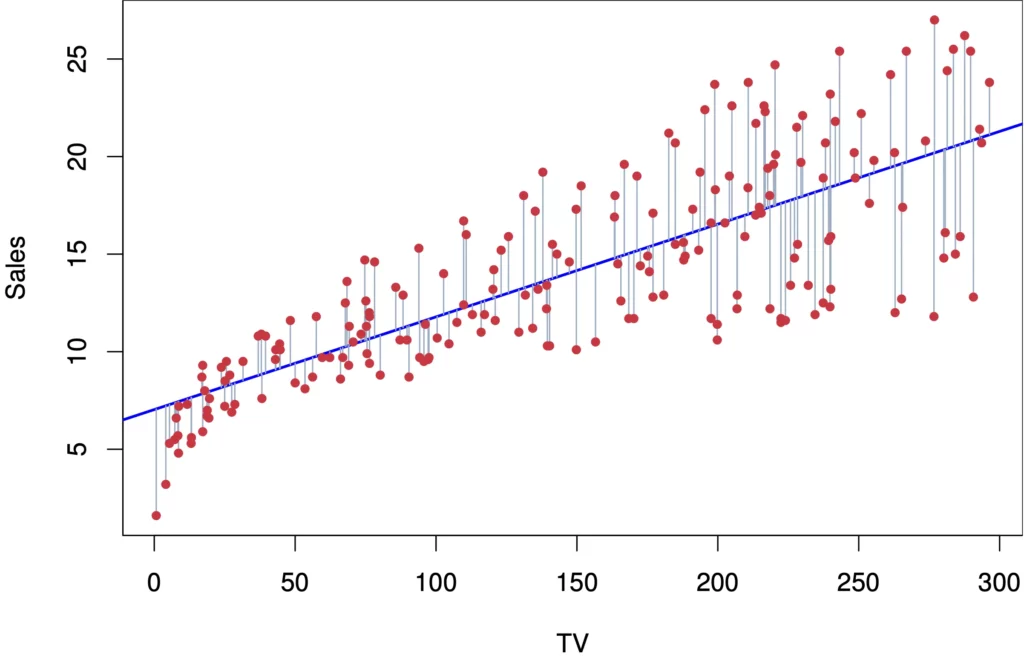
Linear Regression là gì?

Linear Regression là một thuật toán học có giám sát (supervised learning) trong Machine Learning, nó là một phương pháp thống kê dùng để ước lượng mối quan hệ giữa các biến độc lập (input features) và biến phụ thuộc (output target). Linear Regression giả định rằng sự tương quan giữa các biến là tuyến tính, từ đó tìm ra hàm tuyến tính tốt nhất để biểu diễn mối quan hệ này. Thuật toán này dự báo giá trị của biến output từ các giá trị của các biến đầu vào.

Các loại Linear Regression

Có hai loại chính của Linear Regression:

1. Simple Linear Regression: Mô hình này chỉ có một biến độc lập (input feature) mô tả mối quan hệ tuyến tính giữa biến phụ thuộc (output target) và biến độc lập. Phương trình của Simple Linear Regression có dạng y = a + bx + \epsilon, trong đó a là điểm giao với trục tung (chỉ số độc lập), b là hệ số góc (độ dốc) của đường thẳng, và \epsilon là sai số.
2. Multiple Linear Regression: Mô hình này có nhiều hơn một biến độc lập, biểu diễn mối quan hệ tuyến tính giữa các biến độc lập và biến phụ thuộc. Phương trình của Multiple Linear Regression có dạng y = a + b_1x_1 + b_2x_2 + … + b_nx_n + \epsilon, trong đó a là điểm giao với trục tung, b_1, b_2, …, b_n là các hệ số góc, và \epsilon là sai số.

Mục tiêu của Linear Regression

Mục tiêu của Linear Regression là tìm ra hệ số góc và điểm giao với trục tung sao cho hàm dự đoán tuyến tính đạt được sai số nhỏ nhất. Một trong những cách phổ biến để ước lượng các hệ số là sử dụng phương pháp Ordinary Least Squares (OLS), trong đó chúng ta cần tối thiểu hóa tổng bình phương sai số (sum of squared error).

Ứng dụng của Linear Regression

Linear Regression được ứng dụng rộng rãi trong nhiều lĩnh vực, như:

• Dự báo giá cả: dự đoán giá nhà, giá cổ phiếu, giá nhiên liệu dựa trên các yếu tố như vị trí, kích thước, chất lượng, lượng cung cầu, …
• Dự báo điểm số: dự đoán điểm số của học sinh dựa trên thời gian học, nỗ lực, kỹ năng, trình độ giáo viên, …
• Dự báo sản phẩm: dự đoán đầu ra sản xuất dựa trên thời gian, công suất, nguyên liệu, lao động, …
• Phân tích chuỗi thời gian: dự đoán xu hướng và chu kỳ của các chuỗi dữ liệu, như bất động sản, thời tiết, xu hướng sản xuất, …

Công thức toán

Chúng ta xem xét mô hình hồi quy tuyến tính đa biến, phương trình của nó có dạng:

y = a + b_1x_1 + b_2x_2 + … + b_nx_n + \epsilon

Trong phương trình này, a là điểm giao với trục tung, b_1, b_2, …, b_n là các hệ số góc, x_1, x_2, …, x_n là các biến độc lập, và ε là sai số. Mục tiêu của chúng ta là tìm ra các hệ số của phương trình để tối thiểu hóa tổng bình phương sai số (RSS):

RSS = \sum_{i=1}^{m}(y^{(i)} - \hat{y}^{(i)})^2

Trong đó, m là số lượng mẫu dữ liệu, y^{(i)} là giá trị thực tế của biến phụ thuộc tại mẫu thứ i, và ŷ^(i) là giá trị dự đoán tại mẫu thứ i. Để tối thiểu hóa tổng bình phương sai số, chúng ta có thể sử dụng phương pháp Gradient Descent hoặc phương pháp Normal Equation.

Code Python

Cách đơn giản nhất để thực hiện Linear Regression trong Python là sử dụng thư viện scikit-learn, sau đây là ví dụ về cách sử dụng LinearRegression từ thư viện này:

# Import necessary libraries
import numpy as np
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error

# Load data
data = pd.read_csv("your_data.csv")

# Split data into input (X) and output (y)
X = data.drop("your_target_column", axis=1)
y = data["your_target_column"]

# Split data into training and testing set
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)

# Create a Linear Regression model
model = LinearRegression()

# Train the model
model.fit(X_train, y_train)

# Make predictions
y_pred = model.predict(X_test)

# Evaluate the model on the testing set
mse = mean_squared_error(y_test, y_pred)
print("Mean Squared Error:", mse)

Trong ví dụ trên, chúng ta sử dụng thư viện scikit-learn để xây dựng mô hình Linear Regression từ dữ liệu và đánh giá hiệu suất của mô hình bằng cách tính sai số bình phương trung bình (Mean Squared Error) giữa kết quả dự đoán và giá trị thực tế.

Kết luận

Linear Regression là một thuật toán phổ biến và cơ bản trong Machine Learning, giúp ước lượng mối quan hệ tuyến tính giữa các biến đầu vào và biến đầu ra. Hồi quy tuyến tính đơn giản sử dụng một biến đầu vào, trong khi hồi quy tuyến tính đa biến sử dụng nhiều biến đầu vào. Cách tiếp cận này có nhiều ứng dụng trong dự báo, phân tích và tối ưu hóa các bài toán trong thực tế.

Hãy chia sẻ bài viết với những người quan tâm và hãy tiếp tục với các bài viết về Machine learning Cơ Bản của trituenhantao.io đê trang bị cho mình các kiến thức cần thiết.