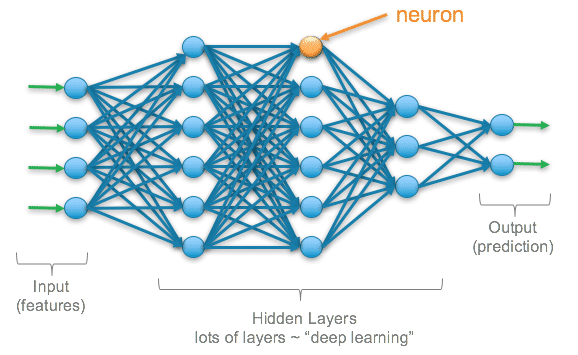
Neural Network (mạng nơ-ron) là mô hình mang lại những kết quả đột phá trong những năm gần đây. Trong bài này, hãy cùng xây dựng Neural Network mà không sử dụng đến các thư viện như TensorFlow hay Pytorch để giúp bạn có thể hiểu rõ hơn về Neural Network.

Mô hình Neural Network được xây dựng như thế nào?

Bạn có thể tưởng tượng đơn giản rằng, Neural Network có cấu trúc gần giống như hệ thần kinh của chúng ta. Thuật toán là một hàm ánh xạ từ bộ dữ liệu đầu vào với kết quả đầu ra tương ứng.

Một mạng nơ-ron gôm những cấu phần sau:

Dữ liệu đầu vào – input layer, x
Lớp ẩn – hidden layers
Dữ liệu đầu ra – output layer, ŷ
Các tham số trọng lượng tương ứng W và ngưỡng quyết định b
Hàm ánh xạ cho lớp ẩn σ . Trong bài này, tôi sẽ chọn hàm Sigmoid

Hình ảnh bên dưới biểu thị mô hình mạng nơ-ron 2 lớp

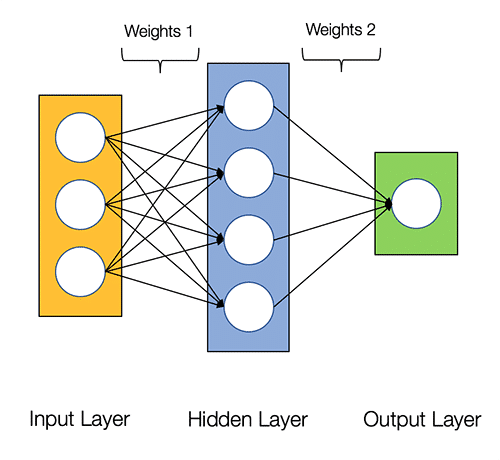
Bạn có thể tạo một mô hình mạng nơ-ron đơn giản trên Python như sau:

class NeuralNetwork:
    def __init__(self, x, y):
        self.input      = x
        self.weights1   = np.random.rand(self.input.shape[1],4) 
        self.weights2   = np.random.rand(4,1)                 
        self.y          = y
        self.output     = np.zeros(y.shape)

Training mô hình mạng nơ-ron

Đầu ra ŷ của mô hình mạng nơ-ron 2 lớp như sau:

$\hat{\mathrm{y}}=\sigma\left(W_2 \sigma\left(W_1 x+b_1\right)+b_2\right)$

Bạn có thể thấy rằng, trọng số W và ngưỡng quyết định b là những yếu tố ảnh hưởng đến kết quả đầu ra ŷ .

Gía trị của trọng số và ngưỡng quyết định sẽ ảnh hưởng tới độ chính xác của mô hình. Qúa trình điều chỉnh hệ số W và b là được gọi là training Neural Network.

Mỗi lần lặp của quá trình bao gồm các bước sau:

Xác định giá trị output đầu ra: output layer, ŷ , được gọi là feedforward
Cập nhật là các trọng số và ngưỡng quyết định (hệ số chặn), được gọi là backpropagation.

Biểu đồ dưới đây minh họa quá trình hoạt động:

Feedforward

Như chúng ta thấy với biểu đồ trên, với mạng nơ ron 2 lớp, feedforward chỉ bao gồm những phép tính cơ bản với đầu ra như sau:

$\hat{y}=\sigma\left(W_2 \sigma\left(W_1 x+b_1\right)+b_2\right)$

Ta thử xây dựng một hàm feedforward trên python như sau:

Lưu ý: giả sử hệ số chặn ở đây bằng 0

class NeuralNetwork:
    def __init__(self, x, y):
        self.input      = x
        self.weights1   = np.random.rand(self.input.shape[1],4) 
        self.weights2   = np.random.rand(4,1)                 
        self.y          = y
        self.output     = np.zeros(self.y.shape)

    def feedforward(self):
        self.layer1 = sigmoid(np.dot(self.input, self.weights1))
        self.output = sigmoid(np.dot(self.layer1, self.weights2))

Tuy nhiên, chúng ta vẫn cần xây dựng một hàm để đánh giá độ chính xác của mô hình. Hàm mất mát chính là một phương pháp cho chúng ta thực hiện điều này.

Loss Function

Có rất nhiều phương thức giúp ta xác định hàm mất mát, điều này tùy thuộc vào lựa chọn của ta. Đơn giản nhất, ta sử dụng Tổng độ lệch bình phương làm hàm mất mát:

$\text { Sum -of-Squares Error }=\sum_{i=1}^n(y-\hat{y})^2$

Tổng độ lệch bình phương là tổng sợ sai khác giữa giá trị dự đoán và giá trị thực tế. Gía trị này được bình phương giúp chúng ta có thể đo được sự sai khác tuyệt đối.

Mục tiêu của chúng ta là tìm ra được hàm Loss Funtion có giá trị nhỏ nhất.

Backpropagation

Sau khi xác định được độ sai lệch giữa hàm dự đoán và thực tế, ta cần truyền lại mô hình và cập nhập lại các trọng số.

Để điều chỉnh được W và b, chúng ta cần mối quan hệ đạo hàm của hàm mất mát với W và b.

Hãy nhớ lại phép tính đạo hàm, ta thấy đạo hàm đơn giản là biểu thị độ dốc của hàm.

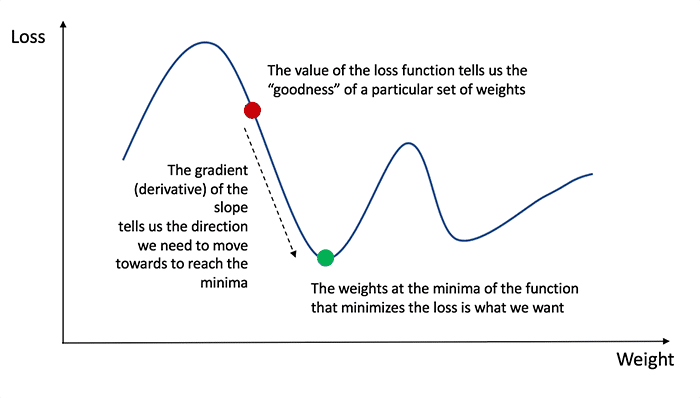
Nếu ta xây dựng được phương trình đạo hàm, ta có thể đơn giản điều chỉnh các hệ số tăng hoặc giảm. Qúa trình này được gọi là gradient descent.

Ngoài ra, ta có thể trực tiếp tính toán hàm đạo hàm thông qua W và b. Tuy nhiên , phương trình của hàm mất mát không có chứa hai hệ số này, nên ta cần xây dựng một công thức để tính toán.

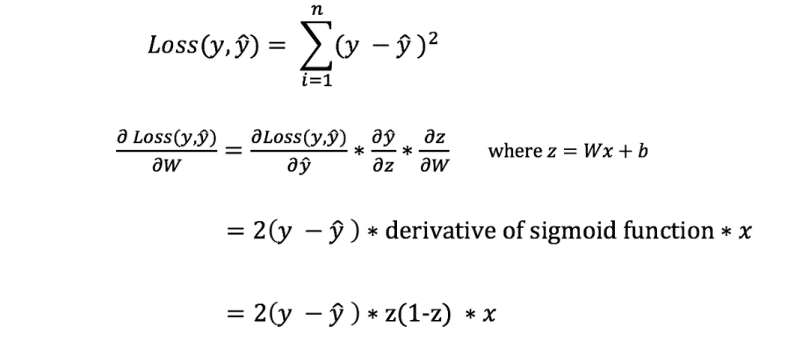
Công thức tính đạo hàm với thông qua các trọng số.
Lưu ý: để đơn giản, công thức này chỉ biểu thị cho mạng nơ-ron 1 lớp

Đây là một phương pháp phức tạp. Tuy nhiên, nó lại là cách giúp ta điều chỉnh lại các hệ số.

Giờ ta hãy xây dựng quy trình này trên python nhé:

class NeuralNetwork:
    def __init__(self, x, y):
        self.input      = x
        self.weights1   = np.random.rand(self.input.shape[1],4) 
        self.weights2   = np.random.rand(4,1)                 
        self.y          = y
        self.output     = np.zeros(self.y.shape)

    def feedforward(self):
        self.layer1 = sigmoid(np.dot(self.input, self.weights1))
        self.output = sigmoid(np.dot(self.layer1, self.weights2))

    def backprop(self):
        # application of the chain rule to find derivative of the loss function with respect to weights2 and weights1
        d_weights2 = np.dot(self.layer1.T, (2*(self.y - self.output) * sigmoid_derivative(self.output)))
        d_weights1 = np.dot(self.input.T,  (np.dot(2*(self.y - self.output) * sigmoid_derivative(self.output), self.weights2.T) * sigmoid_derivative(self.layer1)))

        # update the weights with the derivative (slope) of the loss function
        self.weights1 += d_weights1
        self.weights2 += d_weights2

Để tìm hiểu thêm về ứng dụng toán và quy tắc chuỗi. bạn có thể tham khảo hướng dẫn của
3Blue1Brown.

Xây dựng một ví dụ hoàn chỉnh

Qua hai phần trên, ta đã có code python để thực hiện hai quy trình feedforward và backpropagation. Sử dụng mạng nơ ron mới tạo lập được với một ví dụ, ta có:

. Sử dụng mạng nơ ron mới tạo lập được với một ví dụ, ta có:

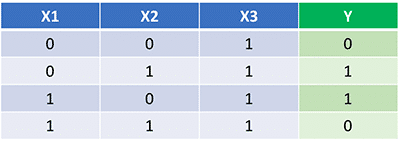
Mạng nơ ron đầu ra là tập hợp những trọng số phù hợp nhất để biểu diễn mối quan hệ trên.

Xây dựng mạng nơ-ron với 1500 lần lặp lại, ta thấy kết quả như sau:

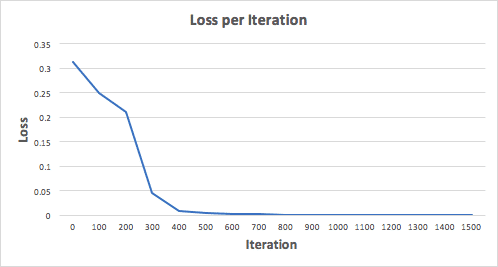
Nhìn vào biều đồ hàm mất mát, ta thấy rõ rằng hàm mất mát giảm dần về giá trị tối thiểu. Điều này là phù hợp với thuật toán gradient descent ta đã trình bày ở trên.

Và đây là kết quả sau khi chạy 1500 lần mô hình:

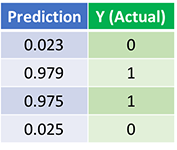
Kết quả thật tuyệt vời. Hai quy trình feedforward và backpropagation đã đưa ra kết quả dần hội tụ với các giá trị thực của chúng.

Lưu ý rằng: giá trị dự đoán và giá trị thực tế luôn có sự khác biệt. Điều này là tốt vì ta có thể tránh được vấn đề overfitting và cho phép mạng nơ ron tổng quát hóa được bộ dữ liệu hơn.

What’s Next?

Hay thật! Mạng nơ ron thực sự chỉ đơn giản vậy thôi. Ngoài những kiến thức trên, bạn có thể tìm hiểu thêm về các vấn đề:

Các hàm kích hoạt (activation function) mạng nơ ron khác ngoài hàm Sigmoid.
Tỷ lệ phù hợp (learning rate)để training mô hình mạng nơ ron.
Sử dụng convolutions trong phân loại hình ảnh.

Ngày nay, các thư viện như TensorFlow, Pytorch hoặc Keras hỗ trợ ta dễ dàng xây dựng mô hình mạng nơ ron, tuy nhiên lại không giúp ta hiểu sâu về cách thức hoạt động. Tôi hi vọn bài này sẽ giúp ích cho bạn.