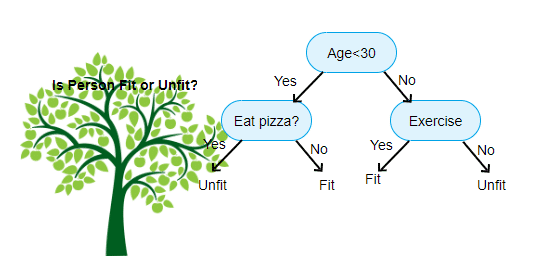
Bạn có biết rằng trong cuộc sống hàng ngày, bạn vẫn đang sử dụng phương pháp Decision Tree (Cây quyết định). Chẳng hạn, bạn đến siêu thị mua sữa cho cả gia đình. Câu đầu tiên trong đầu bạn sẽ là: Bạn cần mua bao nhiêu sữa?
Bạn sẽ xác định: Nếu là ngày thường thì gia đình bạn sẽ sử dụng hết 1 lít sữa, còn cuối tuần thì sẽ là 1,5 lít. Như vậy, dựa theo ngày, bạn sẽ quyết định lượng thực phẩm cần mua cho gia đình bạn.
Đó chính là một dạng của cây quyết định nhị phân.
Khái niệm Cây quyết định (Decision Tree)
Cây quyết định (Decision Tree) là một cây phân cấp có cấu trúc được dùng để phân lớp các đối tượng dựa vào dãy các luật. Các thuộc tính của đối tượngncó thể thuộc các kiểu dữ liệu khác nhau như Nhị phân (Binary) , Định danh (Nominal), Thứ tự (Ordinal), Số lượng (Quantitative) trong khi đó thuộc tính phân lớp phải có kiểu dữ liệu là Binary hoặc Ordinal.
Tóm lại, cho dữ liệu về các đối tượng gồm các thuộc tính cùng với lớp (classes) của nó, cây quyết định sẽ sinh ra các luật để dự đoán lớp của các dữ liệu chưa biết.
Ta hãy xét một ví dụ 1 kinh điển khác về cây quyết định. Giả sử dựa theo thời tiết mà các bạn nam sẽ quyết định đi đá bóng hay không?
Những đặc điểm ban đầu là:
- Thời tiết
- Độ ẩm
- Gió
Dựa vào những thông tin trên, bạn có thể xây dựng được mô hình như sau:
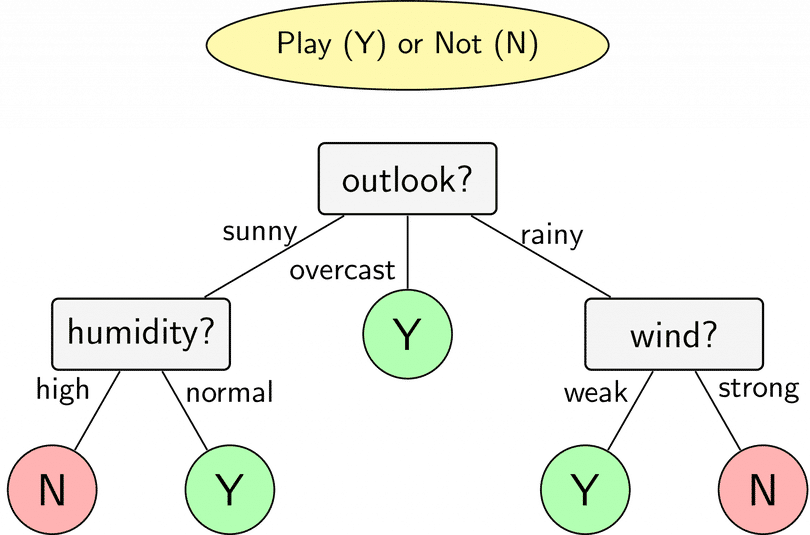
Dựa theo mô hình trên, ta thấy:
Nếu trời nắng, độ ẩm bình thường thì khả năng các bạn nam đi chơi bóng sẽ cao. Còn nếu trời nắng, độ ẩm cao thì khả năng các bạn nam sẽ không đi chơi bóng.
Thuật toán Cây quyết định (Decision Tree)
Thuật toán ID3
Giờ chúng ta hãy cùng tìm hiểu cách thức hoạt động của thuật toán cây quyết định thông qua thuật toán đơn giản ID3.
ID3 (J. R. Quinlan 1993) sử dụng phương pháp tham lam tìm kiếm từ trên xuống thông qua không gian của các nhánh có thể không có backtracking. ID3 sử dụng Entropy và Information Gain để xây dựng một cây quyết định.
Ta xét ví dụ 2:
Bạn muốn xem xét sự thành công của một bộ phim thông qua hai yếu tố: diễn viên chính của phim và thể loại phim:
| Lead Actor | Genre | Hit(Y/N) |
|---|---|---|
| Amitabh Bacchan | Action | Yes |
| Amitabh Bacchan | Fiction | Yes |
| Amitabh Bacchan | Romance | No |
| Amitabh Bacchan | Action | Yes |
| Abhishek Bacchan | Action | No |
| Abhishek Bacchan | Fiction | No |
| Abhishek Bacchan | Romance | Yes |
Giả sử, bạn muốn xác định độ thành công của bộ phim chỉ trên 1 yếu tố, bạn sẽ có hai cách thực hiện sau: qua diễn viên chính của phim và qua thể loại phim.
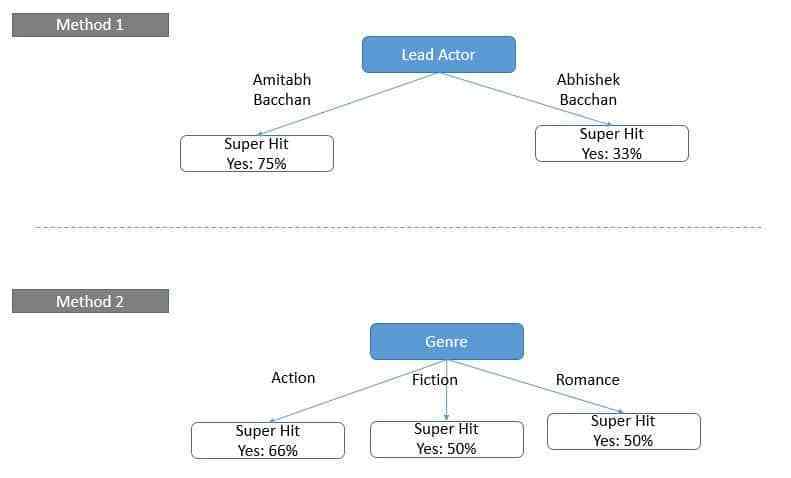
Qua sơ đồ, ta có thể thấy rõ ràng ràng, với phương pháp thứ nhất, ta phân loại được rõ ràng, trong khi phương pháp thứ hai, ta có một kết quả lộn xộn hơn. Và tương tự, cây quyết định sẽ thực hiện như trên khi thực hiện việc chọn các biến.
Có rất nhiều hệ số khác nhau mà phương pháp cây quyết định sử dụng để phân chia. Dưới đây, tôi sẽ đưa ra hai hệ số phổ biến là Information Gain và Gain Ratio (ngoài ra còn hệ số Gini).
Entropy trong Cây quyết định (Decision Tree)
Entropy là thuật ngữ thuộc Nhiệt động lực học, là thước đo của sự biến đổi, hỗn loạn hoặc ngẫu nhiên. Năm 1948, Shannon đã mở rộng khái niệm Entropy sang lĩnh vực nghiên cứu, thống kê với công thức như sau:
Với một phân phối xác suất của một biến rời rạc x có thể nhận n giá trị khác nhau x1,x2,…,xn.
Giả sử rằng xác suất để x nhận các giá trị này là pi=p(x=xi).
Ký hiệu phân phối này là p=(p1 ,p2 ,…,pn). Entropy của phân phối này được định nghĩa là:
H(p)= – ∑nn=1 pi log(pi)
Giả sử bạn tung một đồng xu, entropy sẽ được tính như sau:
H = -[0.5 ln(0.5) + 0.5 ln(0.5)]
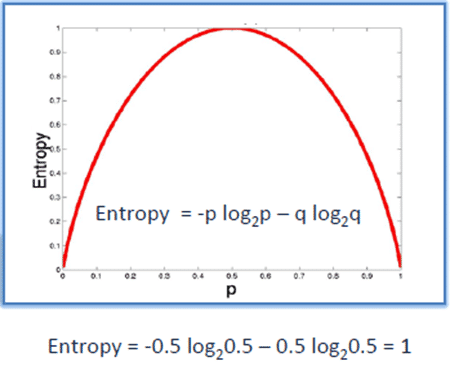
Hình vẽ trên biểu diễn sự thay đổi của hàm entropy. Ta có thể thấy rằng, entropy đạt tối đa khi xác suất xảy ra của hai lớp bằng nhau.
- P tinh khiết: pi = 0 hoặc pi = 1
- P vẩn đục: pi = 0.5, khi đó hàm Entropy đạt đỉnh cao nhất
Information Gain trong Cây quyết định (Decision Tree)
Information Gain dựa trên sự giảm của hàm Entropy khi tập dữ liệu được phân chia trên một thuộc tính. Để xây dựng một cây quyết định, ta phải tìm tất cả thuộc tính trả về Infomation gain cao nhất.
Để xác định các nút trong mô hình cây quyết định, ta thực hiện tính Infomation Gain tại mỗi nút theo trình tự sau:
•Bước 1: Tính toán hệ số Entropy của biến mục tiêu S có N phần tử với Nc phần tử thuộc lớp c cho trước:
H(S)= – ∑cc=1 (Nc/N) log(Nc/N)
•Bước 2: Tính hàm số Entropy tại mỗi thuộc tính: với thuộc tính x, các điểm dữ liệu trong S được chia ra K child node S1, S2, …, SK với số điểm trong mỗi child node lần lượt là m1, m2 ,…, mK , ta có:
H(x, S) = ∑Kk=1 (mk / N) * H(Sk )
Bước 3: Chỉ số Gain Information được tính bằng:
G(x, S) = H(S) – H(x,S)
Với ví dụ 2 trên, ta tính được hệ số Entropy như sau:
EntropyParent = -(0.57*ln(0.57) + 0.43*ln(0.43)) = 0.68
Hệ số Entropy theo phương pháp chia thứ nhất:
Entropyleft = -(.75*ln(0.75) + 0.25*ln(0.25)) = 0.56
Entropyright = -(.33*ln(0.33) + 0.67*ln(0.67)) = 0.63
Ta có thể tính hệ số Information Gain như sau:
Information Gain = 0.68 – (4*0.56 + 3*0.63)/7 = 0.09
Hệ số Entropy với phương pháp chia thứ hai như sau:
Entropyleft = -(.67*ln(0.67) + 0.33*ln(0.33)) = 0.63
Entropymiddle = -(.5*ln(0.5) + 0.5*ln(0.5)) = 0.69
Entropyright = -(.5*ln(0.5) + 0.5*ln(0.5)) = 0.69
Hệ số Information Gain:
Information Gain = 0.68 – (3*0.63 + 2*0.69 + 2*0.69)/7 = 0.02
So sánh kết quả, ta thấy nếu chia theo phương pháp 1 thì ta được giá trị hệ số Information Gain lớn hơn gấp 4 lần so với phương pháp 2. Như vậy, giá trị thông tin ta thu được theo phương pháp 1 cũng nhiều hơn phương pháp 2.
Thuật toán C4.5
Thuật toán C4.5 là thuật toán cải tiến của ID3.
Trong thuật toán ID3, Information Gain được sử dụng làm độ đo. Tuy nhiên, phương pháp này lại ưu tiên những thuộc tính có số lượng lớn các giá trị mà ít xét tới những giá trị nhỏ hơn. Do vậy, để khắc phục nhược điểm trên, ta sử dụng độ đo Gain Ratio (trong thuật toán C4.5) như sau:
Đầu tiên, ta chuẩn hoá information gain với trị thông tin phân tách (split information):
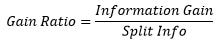
Trong đó: Split Info được tính như sau:
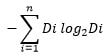
Giả sử chúng ta phân chia biến thành n nút cón và Di đại diện cho số lượng bản ghi thuộc nút đó. Do đó, hệ số Gain Ratio sẽ xem xét được xu hướng phân phối khi chia cây.
Áp dụng cho ví dụ trên và với cách chia thứ nhất, ta có
Split Info = – ((4/7)*log2(4/7)) – ((3/7)*log2(3/7)) = 0.98
Gain Ratio = 0.09/0.98 = 0.092
Tiêu chuẩn dừng
Trong các thuật toán Decision tree, với phương pháp chia trên, ta sẽ chia mãi các node nếu nó chưa tinh khiết. Như vậy, ta sẽ thu được một tree mà mọi điểm trong tập huấn luyện đều được dự đoán đúng (giả sử rằng không có hai input giống nhau nào cho output khác nhau). Khi đó, cây có thể sẽ rất phức tạp (nhiều node) với nhiều leaf node chỉ có một vài điểm dữ liệu. Như vậy, nhiều khả năng overfitting sẽ xảy ra.
Để tránh trường họp này, ta có thể dừng cây theo một số phương pháp sau đây:
- nếu node đó có entropy bằng 0, tức mọi điểm trong node đều thuộc một class.
- nếu node đó có số phần tử nhỏ hơn một ngưỡng nào đó. Trong trường hợp này, ta chấp nhận có một số điểm bị phân lớp sai để tránh overfitting. Class cho leaf node này có thể được xác định dựa trên class chiếm đa số trong node.
- nếu khoảng cách từ node đó đến root node đạt tới một giá trị nào đó. Việc hạn chế chiều sâu của tree này làm giảm độ phức tạp của tree và phần nào giúp tránh overfitting.
- nếu tổng số leaf node vượt quá một ngưỡng nào đó.
- nếu việc phân chia node đó không làm giảm entropy quá nhiều (information gain nhỏ hơn một ngưỡng nào đó).
Ngoài ra, ta còn có phương pháp cắt tỉa cây.
Một số thuật toán khác
Ngoài ID3, C4.5, ta còn một số thuật toán khác như:
- Thuật toán CHAID: tạo cây quyết định bằng cách sử dụng thống kê chi-square để xác định các phân tách tối ưu. Các biến mục tiêu đầu vào có thể là số (liên tục) hoặc phân loại.
- Thuật toán C&R: sử dụng phân vùng đệ quy để chia cây. Tham biến mục tiêu có thể dạng số hoặc phân loại.
- MARS
- Conditional Inference Trees
Ưu/nhược điểm của thuật toán cây quyết định
Ưu điểm
Cây quyết định là một thuật toán đơn giản và phổ biến. Thuật toán này được sử dụng rộng rãi bới những lợi ích của nó:
- Mô hình sinh ra các quy tắc dễ hiểu cho người đọc, tạo ra bộ luật với mỗi nhánh lá là một luật của cây.
- Dữ liệu đầu vào có thể là là dữ liệu missing, không cần chuẩn hóa hoặc tạo biến giả
- Có thể làm việc với cả dữ liệu số và dữ liệu phân loại
- Có thể xác thực mô hình bằng cách sử dụng các kiểm tra thống kê
- Có khả năng là việc với dữ liệu lớn
Nhược điểm
Kèm với đó, cây quyết định cũng có những nhược điểm cụ thể:
- Mô hình cây quyết định phụ thuộc rất lớn vào dữ liệu của bạn. Thạm chí, với một sự thay đổi nhỏ trong bộ dữ liệu, cấu trúc mô hình cây quyết định có thể thay đổi hoàn toàn.
- Cây quyết định hay gặp vấn đề overfitting
Cài đặt cây quyết định với sklearn
Trên đây là những điểm lưu ý khi bạn thực hiện thuật toán cây quyết định.
Hãy theo dõi https://trituenhantao.io/ để có thêm những bài viết hay mới.