Phân phối chuẩn và ứng dụng trong Machine Learning

Phân phối chuẩn hay phân phối Gauss là một khái niệm quan trọng trong thống kê và là nền tảng của Machine Learning. Một Nhà khoa học dữ liệu (Data Scientist) cần biết về phân phối này khi họ làm việc với các mô hình tuyến tính.

Như được Carl Friedrich Gauss khám phá ra, Phân bố chuẩn (Gaussian Distribution) là một phân phối xác suất liên tục. Nó có đường cong hình chuông đối xứng từ điểm trung bình đến cả hai nửa của đường cong.

Định nghĩa toán học của phân phối chuẩn

Một biến ngẫu nhiên liên tục “x” được cho là tuân theo phân phối chuẩn với tham số μ (trung bình) và σ (độ lệch chuẩn) nếu hàm mật độ xác suất của nó được trình bày bởi công thức:

f(x) = \frac{1}{\sigma \sqrt{2 \pi}} e^{ -\frac{1}{2} ( \frac{x-\mu}{\sigma})^2 }

Đây còn được gọi là biến chuẩn (normal variate).

Biến chuẩn hóa (Standard Normal Variate):
Nếu “x” là một biến chuẩn với trung bình (μ) và độ lệch chuẩn (σ) thì:

z = \frac{x-\mu}{\sigma}

Phân phối chuẩn hóa (Standard Normal Distribution)

Trường hợp đơn giản nhất của phân phối chuẩn, được gọi là Phân phối chuẩn hóa (Standard Normal Distribution), có giá trị kỳ vọng μ (trung bình) bằng 0 và σ (độ lệch chuẩn) bằng 1, và được mô tả bởi hàm mật độ xác suất này:

f(z) = \frac{1}{\sqrt{2 \pi}} e^{-\frac{1}{2}z^2}

Các đặc điểm của đường cong phân phối:

• Tổng diện tích dưới đường cong chuẩn bằng 1.
• Đây là phân phối liên tục.
• Nó đối xứng xung quanh giá trị trung bình. Mỗi nửa của phân phối là hình ảnh soi gương của nửa còn lại.
• Nó tiệm cận với trục ngang.
• Nó có một chế độ.

Phân phối chuẩn và các tính chất của diện tích

Phân phối chuẩn đi kèm với các giả định và có thể được chỉ định hoàn toàn bởi hai tham số: trung bình và độ lệch chuẩn. Nếu biết trung bình và độ lệch chuẩn, bạn có thể truy cập tất cả các điểm dữ liệu trên đường cong.

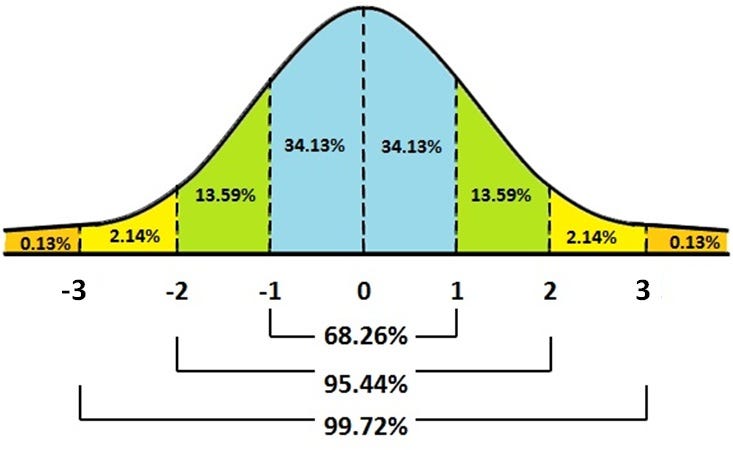
Quy tắc thực nghiệm (Empirical rule) là một ước lượng thuận tiện và nhanh chóng về phạm vi dữ liệu dựa trên trung bình và độ lệch chuẩn của một tập dữ liệu tuân theo phân phối chuẩn. Nó khẳng định rằng:

• 68,26% dữ liệu sẽ nằm trong phạm vi 1 độ lệch chuẩn so với trung bình (μ±1σ)
• 95,44% dữ liệu sẽ nằm trong phạm vi 2 độ lệch chuẩn so với trung bình (μ±2σ)
• 99,7% dữ liệu sẽ nằm trong phạm vi 3 độ lệch chuẩn so với trung bình (μ±3σ)
• 95% — (μ±1,96σ)
• 99% — (μ±2,75σ)

Quy tắc này giúp kiểm tra ngoại lệ (Outliers) và rất hữu ích khi xác định tính chuẩn của bất kỳ phân phối nào.

Ứng dụng trong Machine Learning

Trong Machine Learning Machine Learning
Machine learning (học máy) là nghiên cứu khoa học về các thuật toán và mô hình thống kê mà các hệ thống máy tính sử dụng để thực hiện một nhiệm vụ cụ thể một cách hiệu quả mà không cần sử dụng các hướng dẫn rõ ràng, thay vào đó dựa vào các mẫu và suy luận.
, dữ liệu tuân theo phân phối chuẩn rất có lợi cho việc xây dựng mô hình. Nó làm cho việc tính toán dễ dàng hơn. Các mô hình như LDA, Gaussian Naive Bayes, Logistic Regression, Linear Regression, v.v., được tính toán rõ ràng từ giả định rằng phân phối là chuẩn hai biến hoặc đa biến. Ngoài ra, các hàm Sigmoid hoạt động tự nhiên nhất với dữ liệu theo phân phối này.

Nhiều hiện tượng tự nhiên trên thế giới tuân theo phân phối log-chuẩn, chẳng hạn như dữ liệu tài chính và dữ liệu dự báo. Bằng cách áp dụng các kỹ thuật biến đổi, chúng ta có thể chuyển đổi dữ liệu thành phân phối chuẩn. Ngoài ra, nhiều quá trình tuân theo tính chuẩn, chẳng hạn như nhiều lỗi đo lường trong thực nghiệm, vị trí của một hạt phải trải qua quá trình lan tỏa, v.v.

Cho nên, trước khi đi vào việc xây dựng mô hình, việc quan trọng là cần khám phá dữ liệu kỹ càng và kiểm tra các phân phối tiềm ẩn cho mỗi biến.

Lưu ý: Tính chuẩn là một giả định cho các mô hình Machine Learning Machine Learning
Machine learning (học máy) là nghiên cứu khoa học về các thuật toán và mô hình thống kê mà các hệ thống máy tính sử dụng để thực hiện một nhiệm vụ cụ thể một cách hiệu quả mà không cần sử dụng các hướng dẫn rõ ràng, thay vào đó dựa vào các mẫu và suy luận.
. Điều không bắt buộc là dữ liệu luôn phải tuân theo tính chuẩn. Các mô hình ML hoạt động rất tốt trong trường hợp dữ liệu không phân phối chuẩn. Các mô hình như decision tree, XgBoost, không giả định tính chuẩn nào và làm việc trên dữ liệu thô Dữ liệu thô
Dữ liệu thô là bất kỳ đối tượng dữ liệu nào chưa được xử lý kỹ lưỡng (bằng tay hoặc thông qua phần mềm máy tính tự động.)
. Ngoài ra, hồi quy tuyến tính chỉ có hiệu quả về mặt thống kê nếu chỉ có lỗi mô hình là Gaussian, không chính xác là toàn bộ tập dữ liệu.

Kiểm tra phân phối dữ liệu với Python

Phần sau đây sẽ hướng dẫn bạn cách lập trình vẽ biểu đồ Histogram và Kdeplot bằng Python, để kiểm tra tính chuẩn của dữ liệu và giúp bạn chuẩn bị dữ liệu cho việc xây dựng mô hình Machine Learning Machine Learning
Machine learning (học máy) là nghiên cứu khoa học về các thuật toán và mô hình thống kê mà các hệ thống máy tính sử dụng để thực hiện một nhiệm vụ cụ thể một cách hiệu quả mà không cần sử dụng các hướng dẫn rõ ràng, thay vào đó dựa vào các mẫu và suy luận.
.

import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt

# Load dữ liệu Boston Housing Price
url = "https://archive.ics.uci.edu/ml/machine-learning-databases/housing/housing.data"
names = ['CRIM', 'ZN', 'INDUS', 'CHAS', 'NOX', 'RM', 'AGE', 'DIS', 'RAD', 'TAX', 'PTRATIO', 'B', 'LSTAT', 'MEDV']
df = pd.read_csv(url, delim_whitespace=True, names=names)

# Vẽ Histogram cho tất cả các tính năng số
plt.figure(figsize=(12, 9))
for i, feature in enumerate(df.columns):
    plt.subplot(4, 4, i + 1)
    sns.histplot(df[feature], kde=True)
    plt.xlabel(feature)
plt.tight_layout()
plt.show()

# Vẽ Kdeplot cho tất cả các tính năng số
plt.figure(figsize=(12, 9))
for i, feature in enumerate(df.columns):
    plt.subplot(4, 4, i + 1)
    sns.kdeplot(df[feature])
    plt.xlabel(feature)
plt.tight_layout()
plt.show()

Sử dụng đoạn mã trên, bạn có thể kiểm tra tính chuẩn của dữ liệu và đưa ra quyết định về cách xử lý dữ liệu trước khi đưa vào mô hình Machine Learning Machine Learning
Machine learning (học máy) là nghiên cứu khoa học về các thuật toán và mô hình thống kê mà các hệ thống máy tính sử dụng để thực hiện một nhiệm vụ cụ thể một cách hiệu quả mà không cần sử dụng các hướng dẫn rõ ràng, thay vào đó dựa vào các mẫu và suy luận.
. Nhớ kiểm tra ngoại lệ và tiến hành chuẩn hóa hoặc chuyển đổi dữ liệu khi cần thiết.

Cuối cùng, đừng quên thường xuyên ghé trituenhantao.io để cập nhật kiến thức về AI, Machine Learning Machine Learning
Machine learning (học máy) là nghiên cứu khoa học về các thuật toán và mô hình thống kê mà các hệ thống máy tính sử dụng để thực hiện một nhiệm vụ cụ thể một cách hiệu quả mà không cần sử dụng các hướng dẫn rõ ràng, thay vào đó dựa vào các mẫu và suy luận.
và các ngành khoa học máy tính liên quan khác. Chúng tôi cung cấp nhiều bài viết hữu ích, hướng dẫn và nguồn tài liệu đáng tin cậy để giúp bạn nâng cao trình độ chuyên môn và ứng dụng kiến thức vào thực tế.