Kiểm chứng giả thuyết (Hypothesis testing) là công cụ quan trọng để các nhà khoa học dữ liệu có được các kết luận tin cậy về mặt thống kê. Trong bài này, hãy cùng trituenhantao.io tìm hiểu kiểm chứng giả thuyết thông qua ví dụ đơn giản.
Cơ sở của kiểm chứng giả thuyết
Cơ sở của kiểm chứng giả thuyết là (a) Giả thuyết không – Null Hypothesis và (b) Giả thuyết nghịch – Alternative Hypothesis.
Giả thuyết không là một giả thuyết nhàm chán, nó giả định rằng không có gì thú vị xảy ra cả, tất cả đều chỉ là ngẫu nhiên.
Giả thuyết nghịch là giả thuyết ngược lại với giả thuyết không, nó cho rằng các quan sát / hiện tượng và các con số thống kê có thể cho chúng ta hiểu biết sâu sắc về một khía cạnh nào đó chứ không đơn thuần là một sự tình cờ.
Cách tiến hành kiểm chứng giả thuyết
Các nhà thống kê sẽ bắt đầu với một góc nhìn bi quan trước và bắt đầu với Giả thuyết không. Họ sẽ tính một con số thống kê kiểm định (test statistic) với công thức như sau:
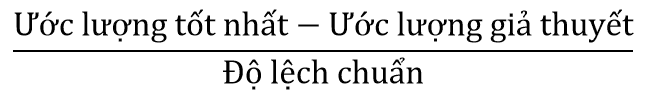
Ở công thức này, ước lượng tốt nhất được tính từ trung bình mẫu hoặc một tổ hợp từ mẫu. Độ lệch chuẩn biểu thị mức độ biến động của ước lượng này và bị ảnh hưởng bởi phương sai và kích thước mẫu.
Sau đó, họ hỏi một câu hỏi đơn giản
“Xác suất để có thể quan sát được con số này là bao nhiêu, liệu con số này có tuyệt đối ngẫu nhiên hay không (nói cách khác là giả thuyết không có đúng hay không)?”
Xác suất để có thể quan sát được con số này được gọi là p-value. Xác suất này được tính trên giả định của một phân phối xác suất nào đó (thường là phân phối chuẩn).
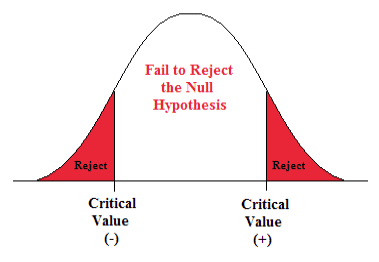
Nếu giả thuyết không là đúng, con số này đơn thuần là một giá trị ngẫu nhiên trong một phân phối xác suất định trước. Phân phối này khác với phân phối của giả thuyết nghịch. Vì vậy, nếu giá trị của đại lượng thống kê kiểm định rơi ra ngoài các giá trị găng (critical value) của phân phối này, thì người ta cho rằng giả thuyết không không đúng.
Trong một số trường hợp, ta dùng cả hai phía của phân phối xác suất. Khi đó ta có kiểm chứng hai phía “two-sided” hoặc kiểm chứng hai đuôi ‘two-tailed’. Trong các trường hợp khác, khi ta chỉ dùng một phía của phân phối xác suất, ta có kiểm chứng một phía hoặc kiểm chứng một đuôi.
Một lưu ý quan trọng là ta không bao giờ có thể chấp nhận Giả thuyết không mà chỉ có thể bác bỏ hoặc thất bại trong việc bác bỏ nó. Khi giả thuyết không được bác bỏ, ta ngầm định chấp nhận giả thuyết nghịch, tức là kết quả quan sát được không phải là một kết quả ngẫu nhiên.
Ví dụ về kiểm chứng giả thuyết
Nếu bạn từng xem phim trên Netflix, bạn chắc chắn đã tham gia vào một hình thức của kiểm chứng giả thuyết mang tên A/B testing.
Netflix hiển thị cùng một chương trình với các thiết kế khác nhau cho các nhóm người dùng khác nhau. Phản ứng của người dùng (như click, không click, xem, quay trở lại) được thu thập và phân tích với phương pháp kiểm chứng giả thuyết.

Ví dụ kiểm chứng giả thuyết với Python
Câu hỏi nghiên cứu: Trong những năm trước, 52% phụ huynh tin rằng thiết bị công nghệ và mạng xã hội khiến cho con mình ở độ tuổi thanh thiếu niên bị thiếu ngủ. Liệu tỷ lệ các phụ huynh ngày nay có niềm tin tương tự có nhiều hơn hay không?
Tổng thể: Phụ huynh có con từ 13–18 tuổi
Khía cạnh quan tâm: p (tỷ lệ)
Giả thuyết không: p = 0.52
Giả thuyết nghịch: p > 0.52 (kiểm chứng một phía)
Dữ liệu: 1018 người tham gia trả lời bảng hỏi. 56% những người tham gia tin rằng con mình ở độ tuổi thanh thiếu niên thiếu ngủ vì mạng xã hội và thiết bị công nghệ.
Tiền hành: Với Python, chúng ta có nhiều thư viện hỗ trợ kiểm chứng giả thuyết. Với bài toán như trên, ta sẽ sử dụng hàm proportions_ztest() từ gói statsmodels. Ta chỉ định alternative="larger" vì đây là kiểm chứng một phía. Hàm sẽ trả về giá trị thống kê kiểm định và p-value.
import statsmodels.api as sm
import numpy as np
import matplotlib.pyplot as plt
n = 1018
pnull = 0.52
phat = 0.56
sm.stats.proportions_ztest(phat * n, n, pnull, alternative='larger')
>> (2.571067795759113, 0.005069273865860533)
Đoạn code trên trả về p-value=0.00507, đây là một giá trị khá nhỏ nên ta có thể bác bỏ Giả thuyết không.
Hi vọng thông qua bài viết này, các bạn đã có hình dung ban đầu về kiểm chứng giả thuyết. Nếu bạn thích bài viết này, đừng ngại chia sẻ với những người quan tâm. Hãy thường xuyên truy cập website để có những kiến thức cập nhật về lĩnh vực.