Bài 7: Thuật toán Perceptron

Trong bài trước, chúng ta đã tìm hiểu về hồi quy logistic, trong bài này, hãy cùng tìm hiểu về thuật toán perceptron, nguồn gốc của các mang nơ ron Nơ ron
Một nơ ron hay tế bào thần kinh nhân tạo (còn được gọi là perceptron) là một hàm toán học. Nó là tổng của một hoặc nhiều yếu tố đầu vào được nhân với các trọng số. Giá trị này sau đó được chuyển đến một hàm phi tuyến tính, được gọi là hàm kích hoạt, để trở thành đầu ra của nơ ron.
mạnh mẽ hiện nay.

Giới thiệu về Perceptron

Perceptron là một trong những thuật toán học máy đầu tiên và đơn giản nhất, được Frank Rosenblatt phát minh vào năm 1957. Nó được thiết kế như một mô hình phân loại nhị phân, nghĩa là dự đoán một trong hai lớp có thể xác định. Mặc dù đơn giản, Perceptron là nguồn cảm hứng cho các mạng neuron sâu ngày nay.

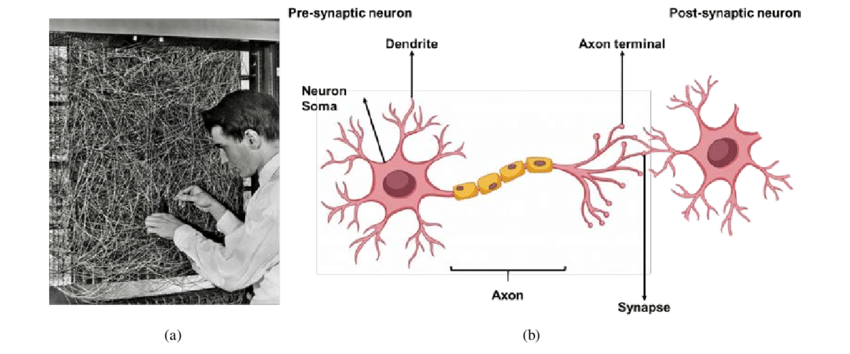
Cấu trúc của Perceptron

Một Perceptron có thể được xem như là một neuron nhân tạo đơn lẻ. Nó bao gồm:

• Đầu vào (inputs): Mỗi đầu vào được đánh trọng số (weights) riêng biệt.
• Tổng trọng số (weighted sum): Tính tổng các đầu vào nhân với trọng số tương ứng.
• Hàm kích hoạt (activation function): Đơn vị tính toán sẽ quyết định neuron có nên được kích hoạt hay không.

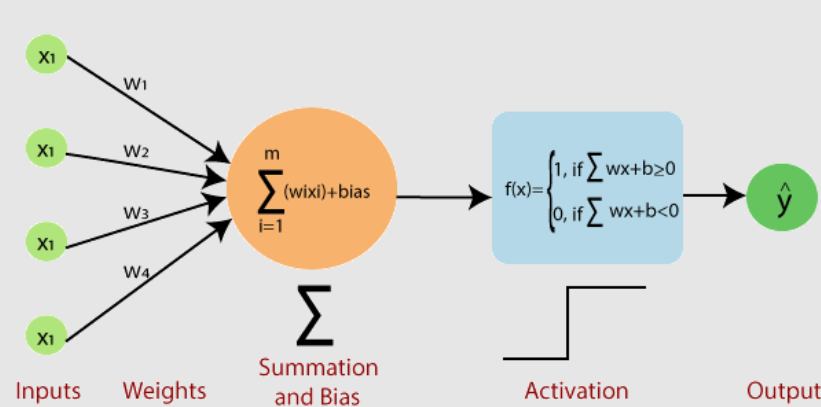
Thông thường, hàm kích hoạt được sử dụng cho Perceptron là hàm step function, nghĩa là nếu tổng trọng số vượt quá một ngưỡng nào đó, đầu ra sẽ là 1 (hoặc lớp A), còn nếu không vượt quá, đầu ra sẽ là -1 (hoặc lớp B).

Thuật toán Perceptron Learning

Thuật toán Perceptron tìm hiểu cách phân chia dữ liệu thành hai lớp bằng cách tìm một “siêu phẳng” (hyperplane) hợp lý. Trong không gian hai chiều, siêu phẳng này là một đường thẳng.

Quá trình học diễn ra qua các bước sau:

1. Khởi tạo trọng số với giá trị nhỏ hoặc bằng không.
2. Với mỗi mẫu trong tập dữ liệu huấn luyện:

• Tính tổng trọng số.
• Áp dụng hàm kích hoạt để nhận được dự đoán.
• Cập nhật trọng số dựa trên sự chênh lệch giữa dự đoán và nhãn thực tế.

1. Lặp lại bước 2 cho đến khi đạt được số lượt lặp tối đa hoặc lỗi trên tập huấn luyện không thay đổi.

Cách cập nhật trọng số

Cập nhật trọng số được thực hiện dựa trên công thức sau:

w_i(t+1) = w_i(t) + η * (y_j - ŷ_j) * x_ij

Trong đó:

• w_i là giá trị trọng số thứ i.
• η là tốc độ học (learning rate Learning rate
  Learning rate - Tốc độ học là một siêu tham số sử dụng trong việc huấn luyện các mạng nơ ron. Giá trị của nó là một số dương, thường nằm trong khoảng giữa 0 và 1. Tốc độ học kiểm soát tốc độ mô hình thay đổi các trọng số để phù hợp với bài toán. Tốc độ học lớn giúp mạng nơ ron được huấn luyện nhanh hơn nhưng cũng có thể làm giảm độ chính xác.
  ), một số thực dương nhỏ.
• y_j là nhãn thực tế của mẫu j.
• ŷ_j là nhãn dự đoán.
• x_ij là giá trị đầu vào thứ i của mẫu j.

Lưu ý khi sử dụng Perceptron

Perceptron chỉ có thể phân loại chính xác khi hai lớp là tuyến tính phân biệt được, tức là có thể tách biệt bằng một đường thẳng. Trong trường hợp dữ liệu không tuyến tính phân biệt, Perceptron sẽ không thể đạt được hội tụ hoàn toàn.

Kết luận

Perceptron là một thuật toán cơ bản và quan trọng trong lịch sử phát triển của Machine Learning Machine Learning
Machine learning (học máy) là nghiên cứu khoa học về các thuật toán và mô hình thống kê mà các hệ thống máy tính sử dụng để thực hiện một nhiệm vụ cụ thể một cách hiệu quả mà không cần sử dụng các hướng dẫn rõ ràng, thay vào đó dựa vào các mẫu và suy luận.
và Neural Networks. Nó đặt nền móng cho sự phát triển của các thuật toán phức tạp hơn như mạng Perceptron đa lớp và sau này là mạng neuron sâu. Hiểu rõ Perceptron và thuật toán học của nó là bước đầu tiên quan trọng trong việc học máy và xây dựng các mô hình AI.