Logic Programming là gì? Nếu bạn đã từng lập trình trước đây, chắc hẳn bạn đã quen thuộc với những ngôn ngữ như là Python, Java, hay C++. Các ngôn ngữ này cho phép chúng ta tạo ra một danh sách các chỉ dẫn để máy tính thực hiện theo. Trong bài viết này, hãy cùng tìm hiểu một nhánh ngôn ngữ lập trình khác mang tên Logic Programming – lập trình dựa trên các quan hệ và suy luận logic với ngôn ngữ tiêu biểu là Prolog.

Các quan hệ

Một trong những khái niệm cơ bản nhất trong logic programming là mối quan hệ. Để có thể hình dung dễ hơn, hãy nhìn vào một dòng code prolog với ví dụ kinh điển.

mortal(X) :- man(X).

Quan hệ được viết bởi “A :- B” được hiểu là “nếu B thì A”. Ví dụ trên nghĩa là “nếu X là người, X sẽ không bất tử” hoặc đơn giản “con người không bất tử”. Dấu chấm đánh dấu kết thúc câu lệnh trong Prolog. Giờ chúng ta bổ sung tiếp dòng code.

man(socrates).

Câu lệnh này có ý nghĩa là “socrates là con người”. Tiếp theo, bạn sẽ thấy được ý nghĩa của các mối quan hệ. Sau khi định nghĩa quan hệ, ta có thể thực hiện được truy vấn, ví dụ như:

?- mortal(socrates).
true.

Kết quả của truy vấn trên là “socrates không bất tử”. Đáp án lấy được từ cơ sở tri thức của chúng ta với hai quan hệ “socrates là con người” và “con người không bất tử”. Ngoài ra, chúng ta có thể liệt kê tất cả những thực thể không bất tử (trong cơ sở tri thức):

?- mortal(X).
X = socrates.

Trong prolog, chữ in hoa để đánh dấu tên biến.

Đồ thị có hướng

Chúng ta có một đồ thị như hình dưới đây. Chúng ta sẽ mô hình hóa và tiến hành suy luận trên đồ thị này.

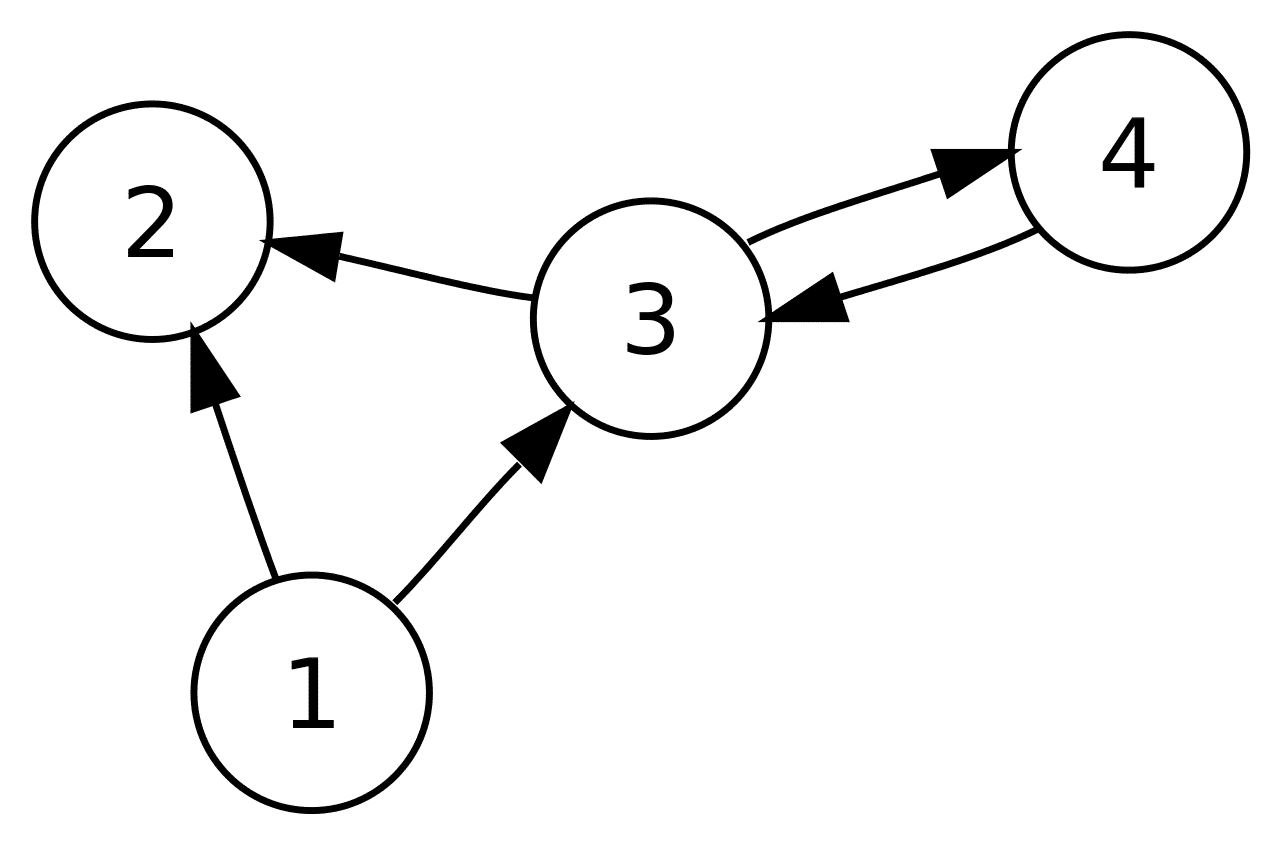
Đầu tiên, chúng ta mô tả đồ thị này. Để làm được như vậy, ta khai báo các quan hệ giữa các đỉnh của đồ thị.

arrow(1,2).
arrow(1,3).
arrow(3,2).
arrow(3,4).
arrow(4,3).

Đây là cách mô tả khá trực quan. Ví dụ, arrow(1,2) nghĩa là có một mũi tên đi từ đình 1 sang đỉnh 2 của đồ thị.

Giả sử như chúng ta muốn biết từ đỉnh A bất kỳ có đường đi đến đỉnh B nào đó hay không. Sẽ có hai khả năng để A đi được đến B, hoặc A và B là hai đỉnh kề nhau hoặc A là đỉnh kề của một đỉnh C nào đó có thể đi được tới B. Ta mô tả trường hợp đầu tiên khá đơn giản:

is_path(A,B) :- arrow(A, B). 

Trường hợp thứ 2 được xử lý như sau:

is_path(A,B) :-
     arrow(A, C),
     is_path(C, B). 

Dấu phẩy thể hiện quan hệ “and” trong prolog. Ví dụ, có đường đi từ 1 đến 4 nếu có một mũi tên từ 1 đến 3 và có đường đi từ 3 đến 4. Sau khi định nghĩa các quan hệ, chúng ta hoàn toàn có thể thực hiện truy vấn như mong muốn.

Lời kết

Qua bài hướng dẫn này, chúng ta đã làm quen với logic programming với hai ví dụ cơ bản. Đây là công cụ giúp ta giải các vấn đề liên quan đến logic. Mặc dù vậy, trong thực tế số lượng các mối quan hệ trong một vấn đề thường là rất lớn nên logic programming thường chỉ áp dụng cho bài toán có phạm vi nhỏ. Nhưng chúng ta cũng không loại trừ khả năng cách tiếp cận này một ngày nào đó lại trở thành xu thế sau nhiều năm không được quan tâm như những gì đã xả ra với mạng nơ ron nhân tạo.