SVM quá khó hiểu! Hãy đọc bài này

SVM SVM
SVM (Support Vector Machine) là một thuật toán học máy có giám sát, sử dụng kỹ thuật ánh xạ dữ liệu vào một không gian nhiều chiều hơn để thuận tiện cho việc tìm ra ranh giới phân chia dữ liệu.
là thuật toán quan trọng trong các thuật toán Học máy. Nó được sử dụng trong cả phân lớp lẫn hồi quy (SVR SVR
SVR (Support Vector Regression) là một mô hình hồi quy sử dụng thuật toán Support Vector Machine (SVM, một thuật toán phân loại) để dự đoán giá trị của một biến liên tục.
). Mặc dù vậy, đằng sau thuật toán này là một loạt các lý thuyết về đại số tuyến tính từ cơ bản đến nâng cao. Nếu bạn đang tìm một bài viết không chứa quá nhiều công thức mà vẫn giúp bạn hiểu được bản chất của SVM SVM
SVM (Support Vector Machine) là một thuật toán học máy có giám sát, sử dụng kỹ thuật ánh xạ dữ liệu vào một không gian nhiều chiều hơn để thuận tiện cho việc tìm ra ranh giới phân chia dữ liệu.
, bài viết này dành cho bạn.

Giới thiệu

Support Vector Machines (có tài liệu dịch là Máy véctơ hỗ trợ) là một trong số những thuật toán phổ biến và được sử dụng nhiều nhất trong học máy trước khi mạng nơ ron Nơ ron
Một nơ ron hay tế bào thần kinh nhân tạo (còn được gọi là perceptron) là một hàm toán học. Nó là tổng của một hoặc nhiều yếu tố đầu vào được nhân với các trọng số. Giá trị này sau đó được chuyển đến một hàm phi tuyến tính, được gọi là hàm kích hoạt, để trở thành đầu ra của nơ ron.
nhân tạo trở lại với các mô hình deep learning Deep Learning
Deep Learning (học sâu) là một lĩnh vực của học máy liên quan đến các thuật toán lấy cảm hứng từ cấu trúc và chức năng của bộ não được gọi là mạng lưới thần kinh nhân tạo.
. Nó được biết đến rộng rãi ngay từ khi mới được phát triển vào những năm 1990.

Mục tiêu của SVM SVM
SVM (Support Vector Machine) là một thuật toán học máy có giám sát, sử dụng kỹ thuật ánh xạ dữ liệu vào một không gian nhiều chiều hơn để thuận tiện cho việc tìm ra ranh giới phân chia dữ liệu.
là tìm ra một siêu phẳng trong không gian N chiều (ứng với N đặc trưng Đặc trưng
Trong học máy và nhận dạng mẫu, một đặc trưng (feature) là một thuộc tính hoặc đặc tính có thể đo lường riêng lẻ của một hiện tượng đang được quan sát.
) chia dữ liệu thành hai phần tương ứng với lớp của chúng. Nói theo ngôn ngữ của đại số tuyển tính, siêu phẳng này phải có lề cực đại và phân chia hai bao lồi và cách đều chúng.

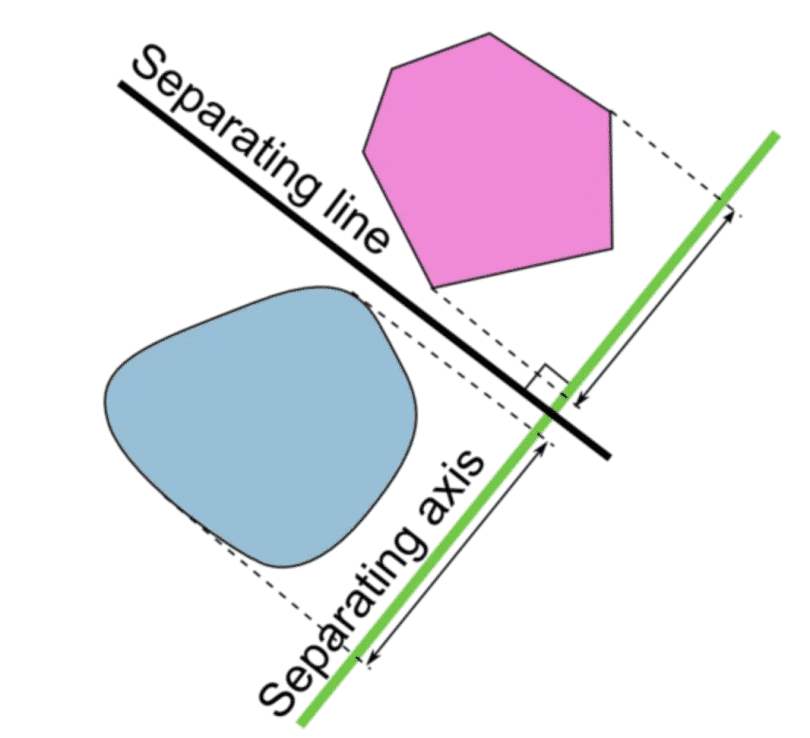
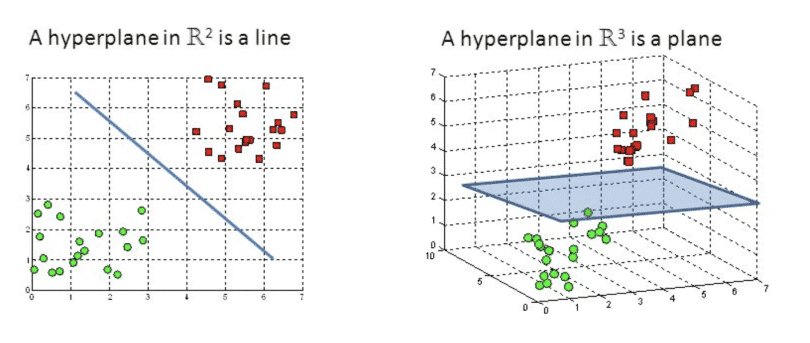
Nếu bạn không quen với đại số tuyến tính, bạn chỉ cần nhớ rằng trong không gian N chiều, một siêu phẳng là một không gian con có kích thước N-1 chiều. Một cách trực quan, trong một mặt phẳng (2 chiều) thì siêu phẳng là một đường thẳng, trong một không gian 3 chiều thì siêu phẳng là một mặt phẳng. Có thể bạn đã biết kiến thức này ở cấp 3 nếu buổi học hôm đó bạn không ngủ gật.

Siêu phẳng tạo ra một biên giới phân chia 2 lớp của dữ liệu.

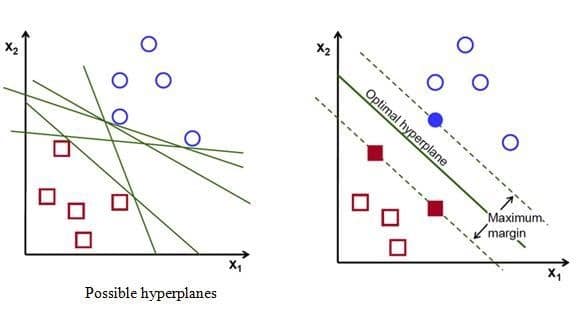
Để phân chia hai lớp dữ liệu, rõ ràng là có rất nhiều siêu phẳng có thể làm được điều này. Mặc dù vậy, mục tiêu của chúng ta là tìm ra siêu phẳng có lề rộng nhất tức là có khoảng cách tới các điểm của hai lớp là lớn nhất. Hình dưới đây là một ví dụ trực quan về điều đó.

Siêu phẳng có lề cực đại trong không gian 3 chiều:

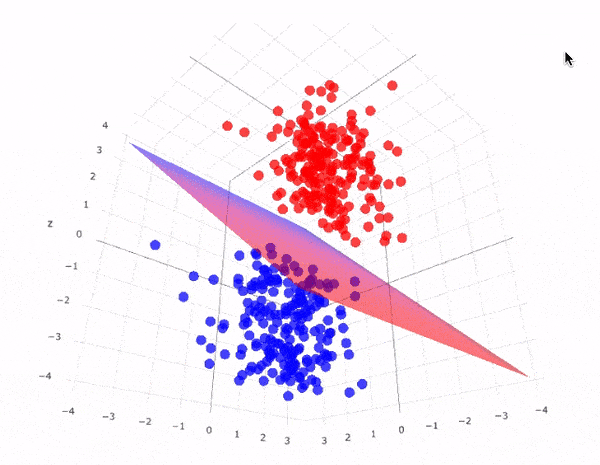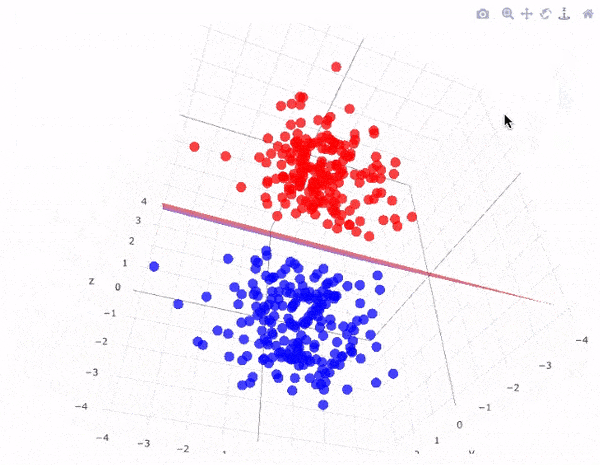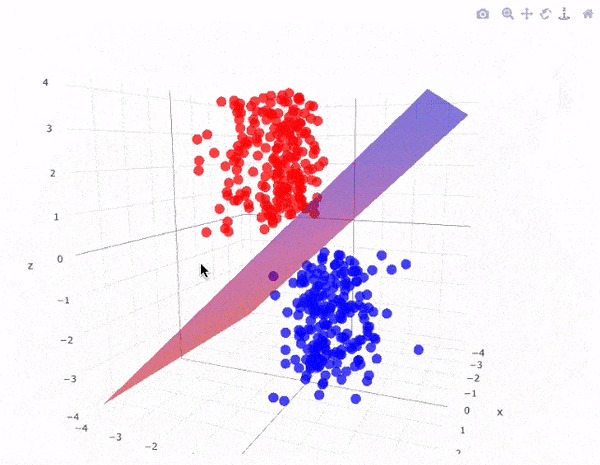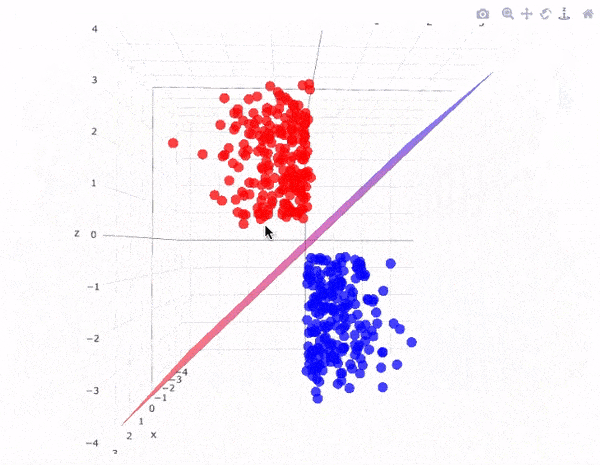
Lưu ý: Số chiều của siêu phẳng phụ thuộc vào số đặc trưng Đặc trưng
Trong học máy và nhận dạng mẫu, một đặc trưng (feature) là một thuộc tính hoặc đặc tính có thể đo lường riêng lẻ của một hiện tượng đang được quan sát.

Các véc tơ hỗ trợ

Một điểm trong không gian véc tơ có thể được coi là một véc tơ từ gốc tọa độ tới điểm đó. Các điểm dữ liệu nằm trên hoặc gần nhất với siêu phẳng được gọi là véc tơ hỗ trợ, chúng ảnh hưởng đến vị trí và hướng của siêu phẳng. Các véc tơ này được sử dụng để tối ưu hóa lề và nếu xóa các điểm này, vị trí của siêu phẳng sẽ thay đổi. Một điểm lưu ý nữa đó là các véc tơ hỗ trợ phải cách đều siêu phẳng.

SVM SVM
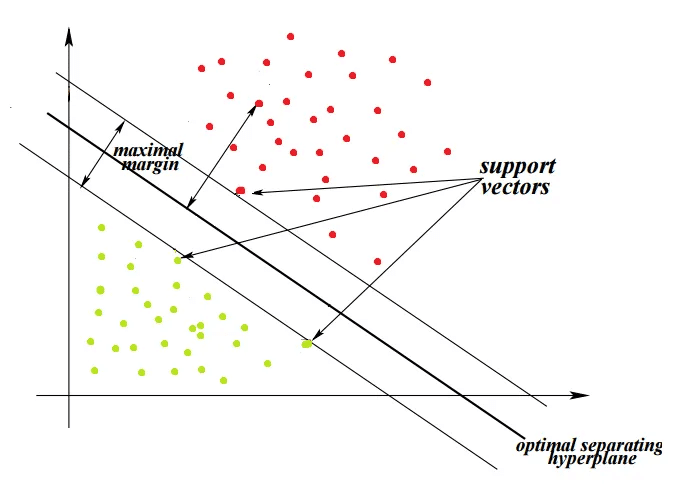
SVM (Support Vector Machine) là một thuật toán học máy có giám sát, sử dụng kỹ thuật ánh xạ dữ liệu vào một không gian nhiều chiều hơn để thuận tiện cho việc tìm ra ranh giới phân chia dữ liệu.
mà chúng ta thảo luận từ đầu bài viết đến giờ chỉ có thể hoạt động trên dữ liệu có thể phân chia tuyến tính.

Nếu dữ liệu không thể phân chia tuyến tính thì sao?

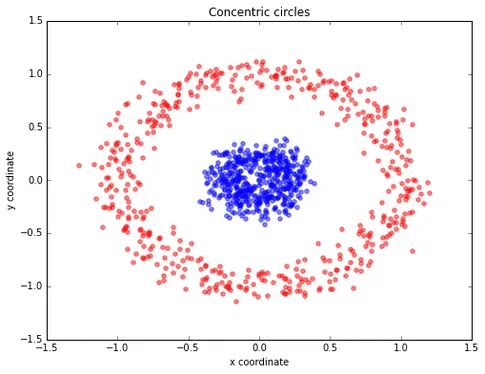
Ví dụ: nhìn vào hình ảnh bên dưới, dữ liệu được phân tách phi tuyến tính, rõ ràng, chúng ta không thể vẽ một đường thẳng để phân loại các điểm dữ liệu đỏ và xanh. Để giải quyết vấn đề này, có hai giải pháp:

1. Lề mềm (Soft margin)
2. Thủ thuật Kernel Kernel
   Kernel là một hàm ánh xạ dữ liệu từ không gian ít nhiều hơn sang không gian nhiều chiều hơn. Đây là kỹ thuật quan trọng trong SVM.
   (Kernel Kernel
   Kernel là một hàm ánh xạ dữ liệu từ không gian ít nhiều hơn sang không gian nhiều chiều hơn. Đây là kỹ thuật quan trọng trong SVM.
   tricks)

Lề mềm

Thuật toán này cho phép SVM SVM
SVM (Support Vector Machine) là một thuật toán học máy có giám sát, sử dụng kỹ thuật ánh xạ dữ liệu vào một không gian nhiều chiều hơn để thuận tiện cho việc tìm ra ranh giới phân chia dữ liệu.
mắc một số lỗi nhất định và giữ cho lề càng rộng càng tốt để các điểm khác vẫn có thể được phân loại chính xác. Nói một cách khác, nó cân bằng giữa việc phân loại sai và tối đa hóa lề.

Có hai kiểu phân loại sai có thể xảy ra:

1. Dữ liệu nằm ở đúng bên nhưng phạm vào lề
2. Dữ liệu nằm ở sai bên

Mức độ chấp nhận lỗi
Mức độ chấp nhận lỗi là một siêu tham số Siêu tham số
Trong học máy, siêu tham số là một tham số có giá trị được đặt trước khi quá trình học bắt đầu. Ngược lại, các giá trị của các tham số khác có được thông qua huấn luyện.
quan trọng trong SVM SVM
SVM (Support Vector Machine) là một thuật toán học máy có giám sát, sử dụng kỹ thuật ánh xạ dữ liệu vào một không gian nhiều chiều hơn để thuận tiện cho việc tìm ra ranh giới phân chia dữ liệu.
. Khi lập trình với sklearn, mức độ chấp nhận lỗi được coi như một tham số phạt (C). Hình dưới thể hiện SVM SVM
SVM (Support Vector Machine) là một thuật toán học máy có giám sát, sử dụng kỹ thuật ánh xạ dữ liệu vào một không gian nhiều chiều hơn để thuận tiện cho việc tìm ra ranh giới phân chia dữ liệu.
với các giá trị C khác nhau.

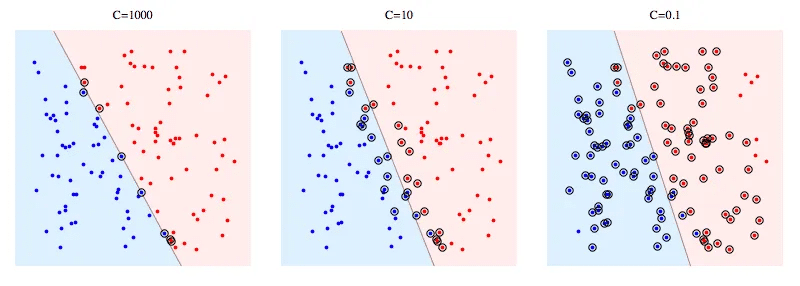
C càng lớn có nghĩa là SVM SVM
SVM (Support Vector Machine) là một thuật toán học máy có giám sát, sử dụng kỹ thuật ánh xạ dữ liệu vào một không gian nhiều chiều hơn để thuận tiện cho việc tìm ra ranh giới phân chia dữ liệu.
càng bị phạt nặng khi thực hiện phân loại sai. Do đó, lề càng hẹp và càng ít vectơ hỗ trợ được sử dụng.

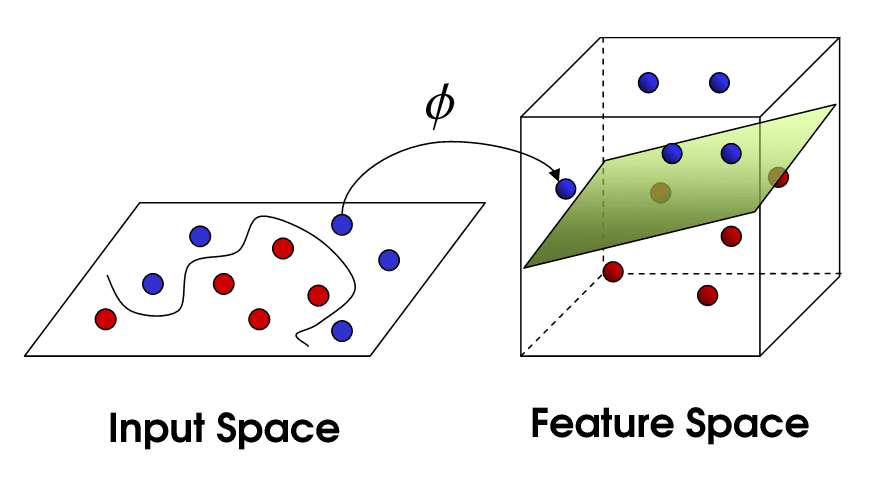
Thủ thuật Kernel Kernel
Kernel là một hàm ánh xạ dữ liệu từ không gian ít nhiều hơn sang không gian nhiều chiều hơn. Đây là kỹ thuật quan trọng trong SVM.

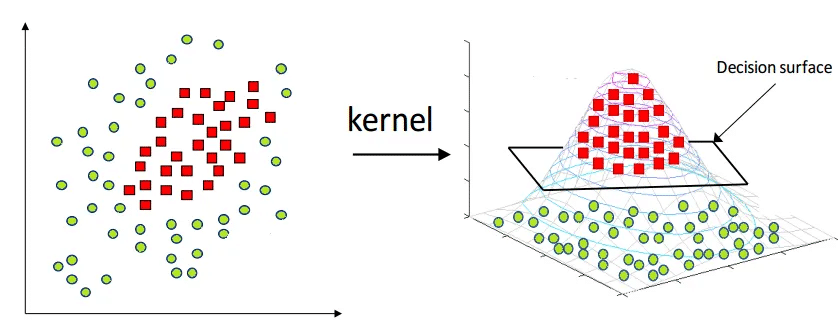
Một kernel Kernel
Kernel là một hàm ánh xạ dữ liệu từ không gian ít nhiều hơn sang không gian nhiều chiều hơn. Đây là kỹ thuật quan trọng trong SVM.
là một hàm ánh xạ dữ liệu từ không gian ít nhiều hơn sang không gian nhiều chiều hơn, từ đó ta tìm được siêu phẳng phân tách dữ liệu. Một cách trực quan, kỹ thuật này giống như việc bạn gập tờ giấy lại để có thể dùng kéo cắt một lỗ tròn trên nó.

Biểu diễn trực quan của thủ thuật kernel Kernel
Kernel là một hàm ánh xạ dữ liệu từ không gian ít nhiều hơn sang không gian nhiều chiều hơn. Đây là kỹ thuật quan trọng trong SVM.
:

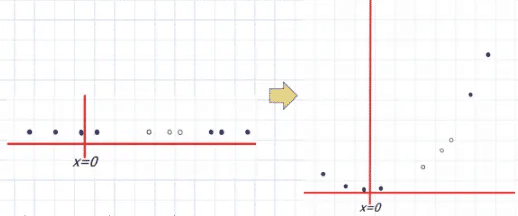
Các kiểu Kernel Kernel
Kernel là một hàm ánh xạ dữ liệu từ không gian ít nhiều hơn sang không gian nhiều chiều hơn. Đây là kỹ thuật quan trọng trong SVM.
:

1. Tuyến tính
2. Đa thức
3. RBF
4. Sigmoid

Hi vọng thông qua bài viết này, bạn đã hiểu hơn về SVM SVM
SVM (Support Vector Machine) là một thuật toán học máy có giám sát, sử dụng kỹ thuật ánh xạ dữ liệu vào một không gian nhiều chiều hơn để thuận tiện cho việc tìm ra ranh giới phân chia dữ liệu.
, một thuật toán mạnh mẽ trong học máy. Nếu bạn thấy bài viết hữu ích, hãy chia sẻ với những người quan tâm hoặc lưu lại để sau này tiện tham khảo.

Hãy thường xuyên truy cập trituenhantao.io hoặc đăng ký (dưới chân trang) để nhận được những bài viết thú vị về Trí tuệ nhân tạo sớm nhất!