Thống kê suy luận là nền tảng cho Trí tuệ nhân tạo cũng như Học máy ngày nay. Hai trường phái triết học nổi tiếng trong thống kê suy luận là Suy luận Frequentist và Suy luận Bayesianist. Điều thú vị là hai trường phái tưởng chừng mâu thuẫn nhau nhưng vẫn tồn tại song song cho đến ngày nay.
Thống kê suy luận là gì?
Hãy tưởng tượng bạn có được các dữ liệu từ việc quan sát những sự vật tồn tại trong cuộc sống, ví dụ như chiều cao của người, số cánh hoa trong mỗi bông hoa, số hot girl theo dõi trận đấu của U23 Việt Nam v..v…
Dữ liệu bạn thu được gọi là các mẫu và bạn có thể tính toán một vài giá trị đặc trưng của mẫu như:
- Giá trị trung bình của mẫu (Trong thống kê gọi là kỳ vọng)
- Độ dao động của mẫu (Trong thống kê gọi là phương sai)
- Số lượng các giá trị lớn hơn và nhỏ hơn giá trị trung bình
- Vân vân và mây mây
Các con số bạn tính ra giúp tổng quát hóa hiểu biết của chúng ta về mẫu đã thu thập được. Phương pháp bạn dùng được gọi là thống kê mô tả (descriptive statistics). Nhưng rõ ràng những con số bạn vừa tính chỉ là một phần nhỏ trong thế giới thực. Bạn nghĩ liệu mình có thể đo được chiều cao của toàn bộ dân số thế giới? Rõ ràng là nếu như chúng ta muốn mở rộng hiểu biết về thế giới thực, chúng ta phải dùng các phương pháp khác. Một trong số những hướng tiếp cận là thống kê suy luận (inferential statistics).
Hai trường phái mâu thuẫn nhau
Một trong những cách giúp tăng hiểu biết của con người về thế giới tự nhiên thông qua những con số toán học, chúng ta có xác suất. Xác suất có thể định nghĩa theo 4 cách:
- Tần suất xảy ra một sự kiện trong dài hạn
- Khuynh hướng của vật chất
- Mức độ của lòng tin về một giả thiết
- Mực độ hợp lý của một giả thiết
Trường phái Frequentist dựa trên định nghĩa đầu tiên. Trong khi đó trường phái Bayesianist dựa trên định nghĩa thứ 3 và 4.
Theo định nghĩa xác suất của Frequentist , chỉ những sự kiện ngẫu nhiên lặp đi lặp lại (như kết quả của việc tung một đồng xu) mới có xác suất. Xác suất này bằng với tần suất xuất hiện trong dài hạn của chúng. Trường phái Frequentist phủ định việc gắn xác suất với các giả thuyết hoặc với bất một giá trị cố định mà chưa biết trước.
Ngược lại, Bayesianist xem xác suất là một khái niệm tổng quát hơn. Xác suất thể hiện sự không chắc chắn trong bất kỳ sự kiện hoặc giả thuyết nào. Trường phái này hoàn toàn chấp nhận việc gán xác suất cho các sự kiện không lặp lại (dựa trên các xác suất tiên nghiệm), ví dụ như sự kiện Hillary Clinton chiến thắng trong cuộc đua vào Nhà Trắng năm 2016.
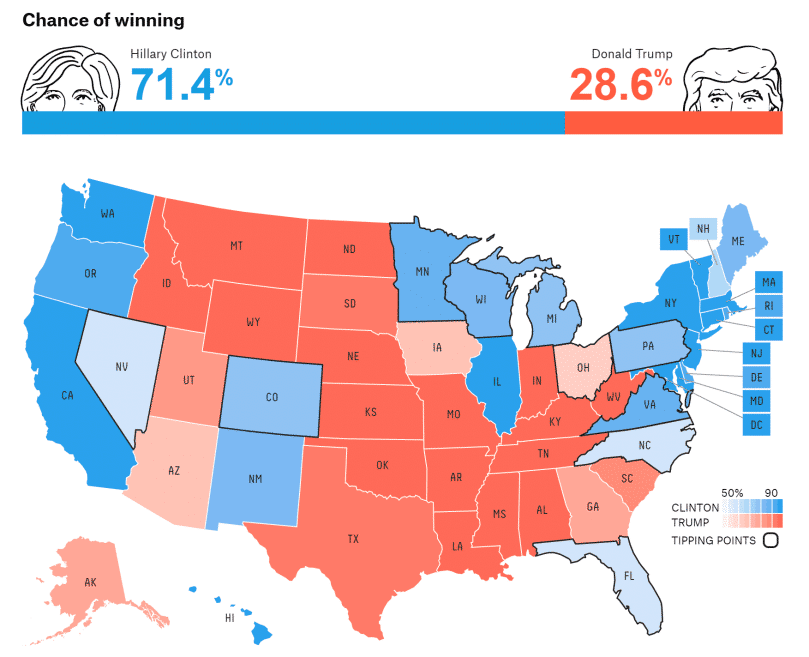
Với trường phái Frequentist, xác suất nói trên không có ý nghĩa gì trừ khi cuộc bầu cử diễn ra với số lần vô hạn và xác suất đó được tính dựa trên tỷ lệ chiến thắng của Hillary Clinton.
Hai trường phái triết học tồn tại song song trong thống kê suy luận quả là thú vị phải không nào? Hãy thường xuyên truy cập trituenhantao.io hoặc đăng ký dưới chân trang để nhận được những bài viết mới nhất và cập nhật về chủ đề này!
